32 R相关与回归
32.1 相关分析
考虑连续型随机变量之间的关系。相关系数定义为 \[\rho(X, Y) = \frac{E\left[ (X - EX)(Y-EY) \right]} {\sqrt{\text{Var}(X)\text{Var}(Y)}} \] 又称Pearson相关系数。
\(-1 \leq \rho \leq 1\)。\(\rho\)接近于\(+1\)表示\(X\)和\(Y\)有正向的相关; \(\rho\)接近于\(-1\)表示\(X\)和\(Y\)有负向的相关。
相关系数代表的是线性相关性, 对于\(X\)和\(Y\)的其它相关可能反映不出来, 比如\(X \sim \text{N}(0,1)\),\(Y = X^2\), 有\(\rho(X, Y) = 0\)。
给定样本\((X_i, Y_i), i=1,2,\dots,n\),样本相关系数为 \[r = \frac{\sum_{i=1}^n (X_i - \bar X) (Y_i - \bar Y)} {\sqrt{\sum_{i=1}^n (X_i - \bar X)^2 \sum_{i=1}^n (Y_i - \bar Y)^2}} \]
用散点图和散点图矩阵直观地查看变量间的相关。
例如,线性相关的模拟数据的散点图:
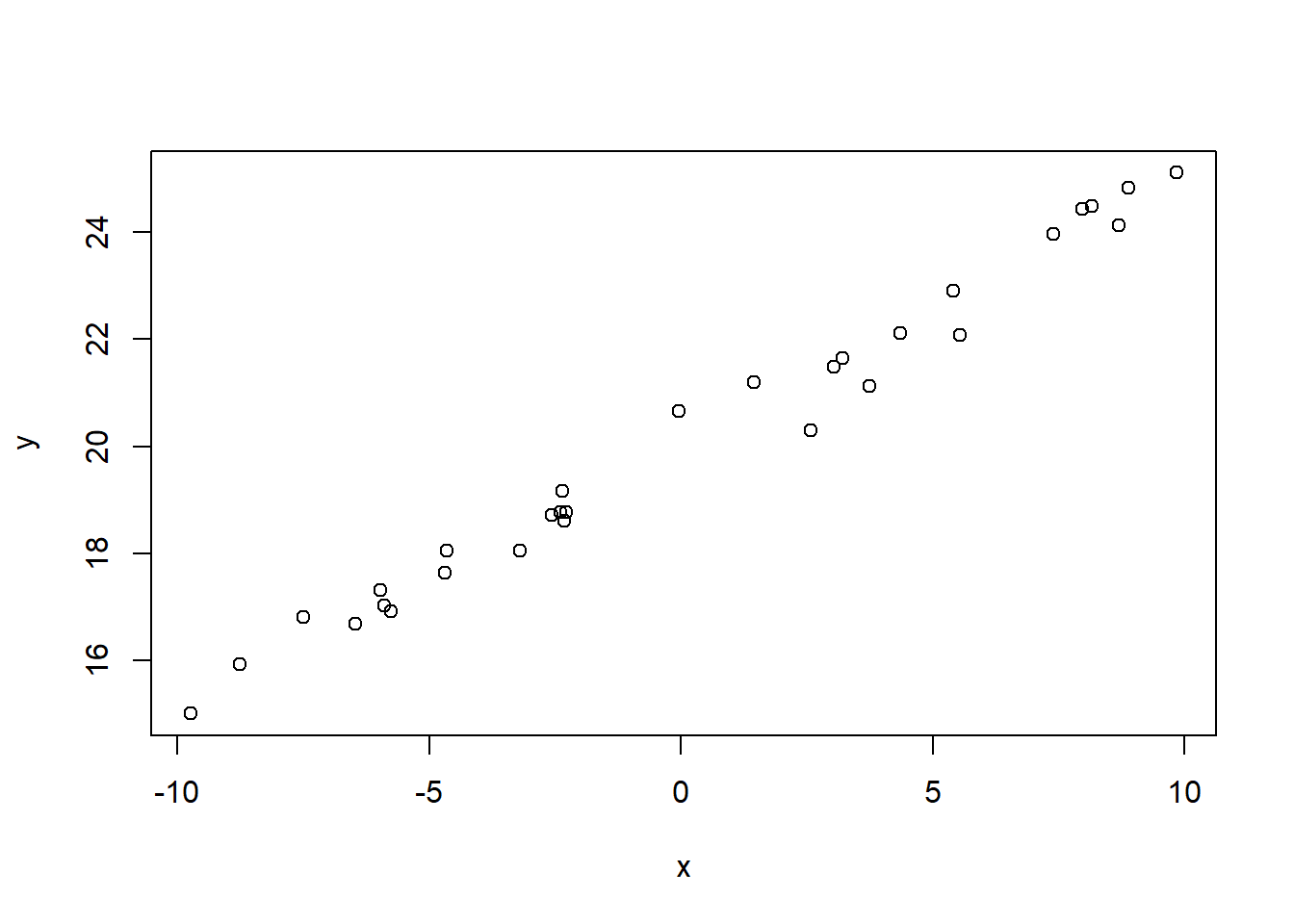
图32.1: 线性相关数据
二次曲线相关的模拟数据散点图:

图32.2: 二次曲线相关数据
指数关系的例子:

图32.3: 指数关系相关数据
对数关系的例子:
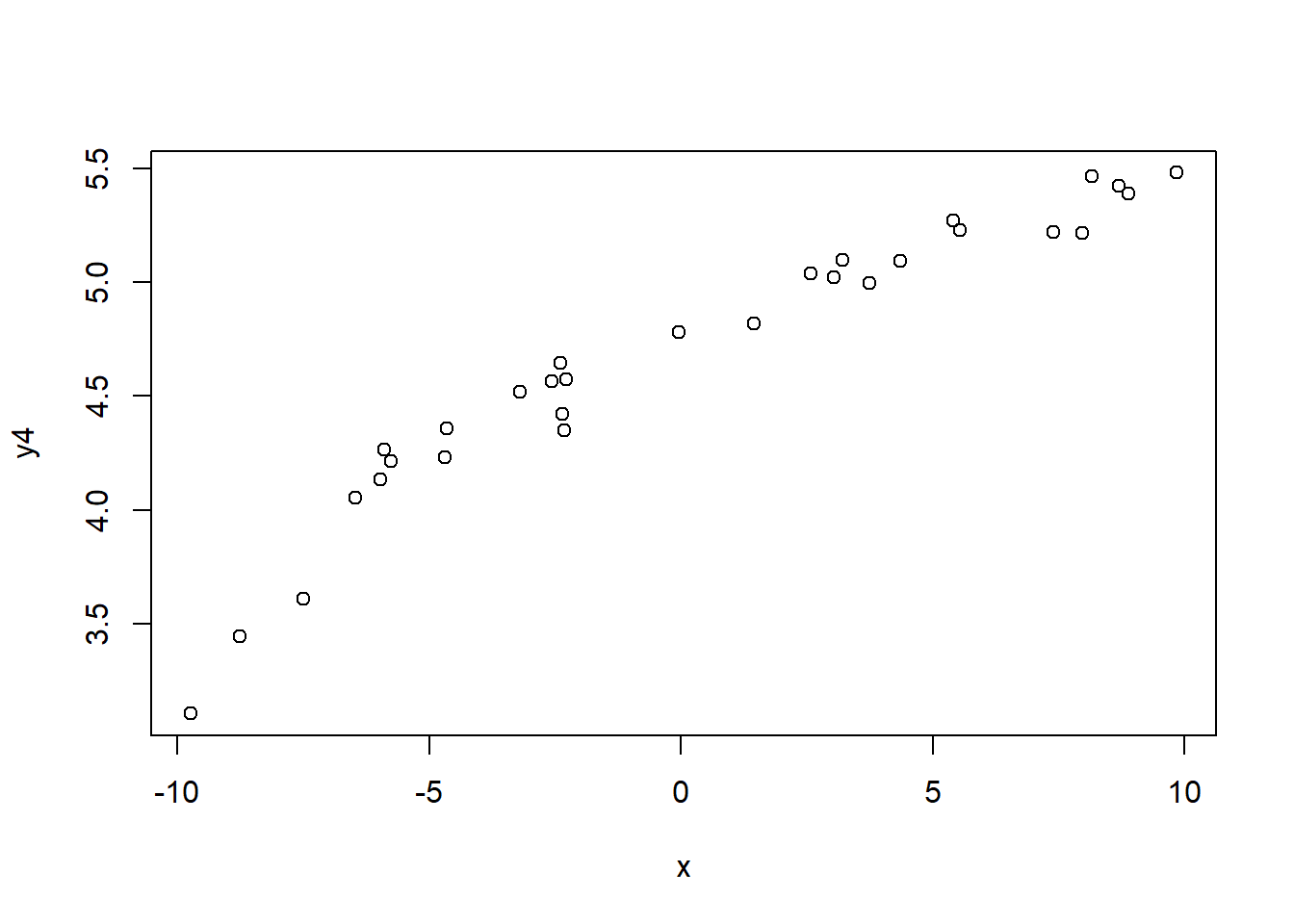
图32.4: 对数关系相关数据
32.1.1 相关系数的性质
- 取值\(-1 \leq r \leq 1\)。
- \(r>0\)表示正线性相关; \(r<0\)表示负线性相关。
- 当\(r=1\)时\((x_i, y_i), i=1,\dots,n\)这\(n\)个点完全在一条正斜率的直线上, 属于确定性关系。
- 当\(r=-1\)时\((x_i, y_i), i=1,\dots,n\)这\(n\)个点完全在一条负斜率的直线上, 属于确定性关系。
- 计算相关系数时与\(x, y\)的次序或记号无关。
- 如果对变量\(x\)或者\(y\)分别乘以倍数,再分别加上不同的平移量, 相关系数不变。 即:\(a + bx\)与\(c + dy\)的相关系数, 等于\(x, y\)的相关系数。 这样,相关系数不受单位、量纲的影响。 相关系数是无量纲的。
- 如果\(x\)和\(y\)之间是非线性相关, 相关系数不一定能准确反映其关系, 只能作为一定程度的近似。
设变量\(X\)和\(Y\)的样本存放于R向量x和y中,
用cor(x,y)计算样本相关系数。
set.seed(1)
x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40 - (x-7)^2 + rnorm(30)
yy <- 40 - (xx-7)^2
plot(x, y, pch=16)
lines(xx, yy)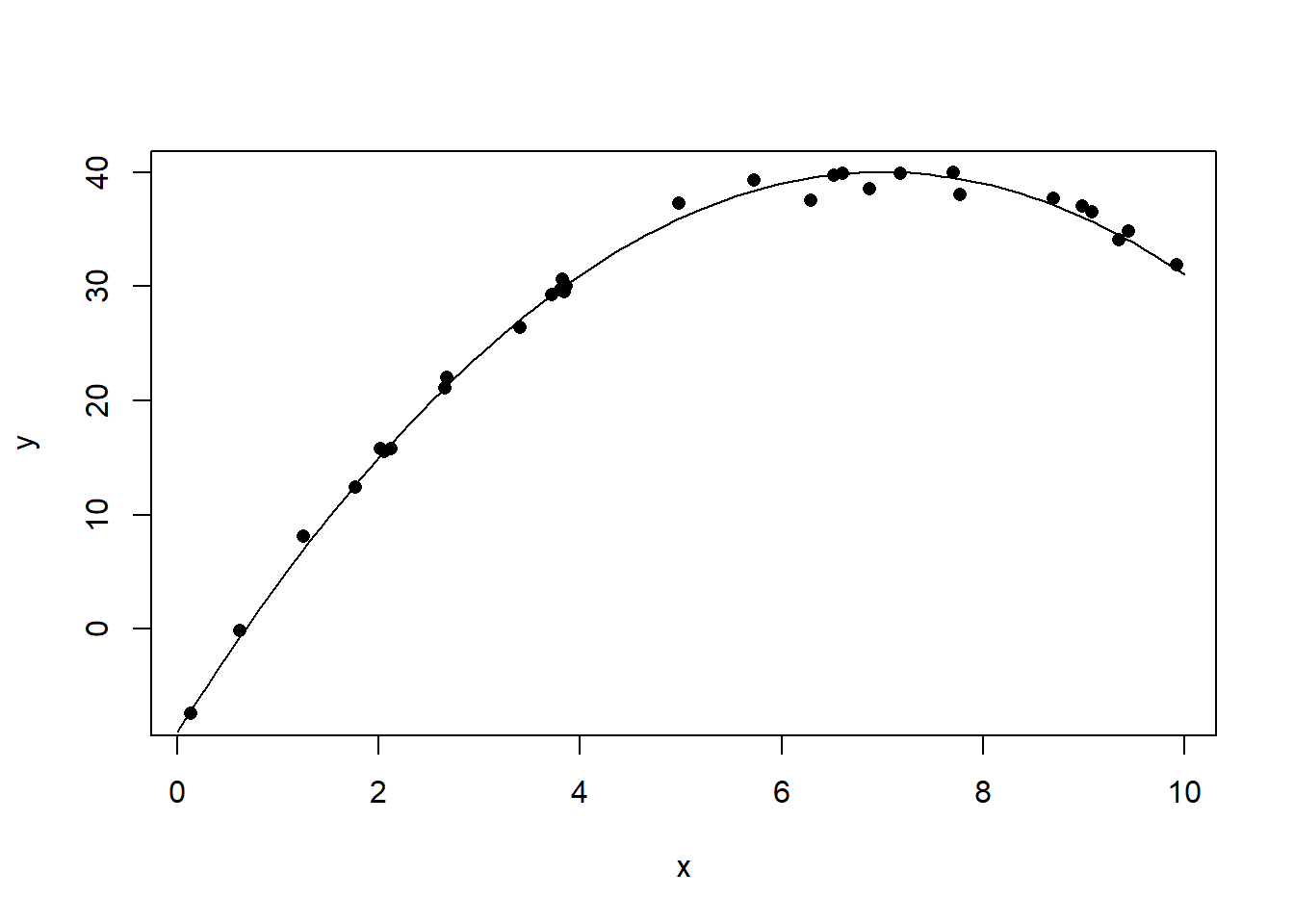
图32.5: 曲线相关数据的相关系数例1
## [1] 0.8244374x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40 - (x-5)^2 + rnorm(30)
yy <- 40 - (xx-5)^2
plot(x, y, pch=16)
lines(xx, yy)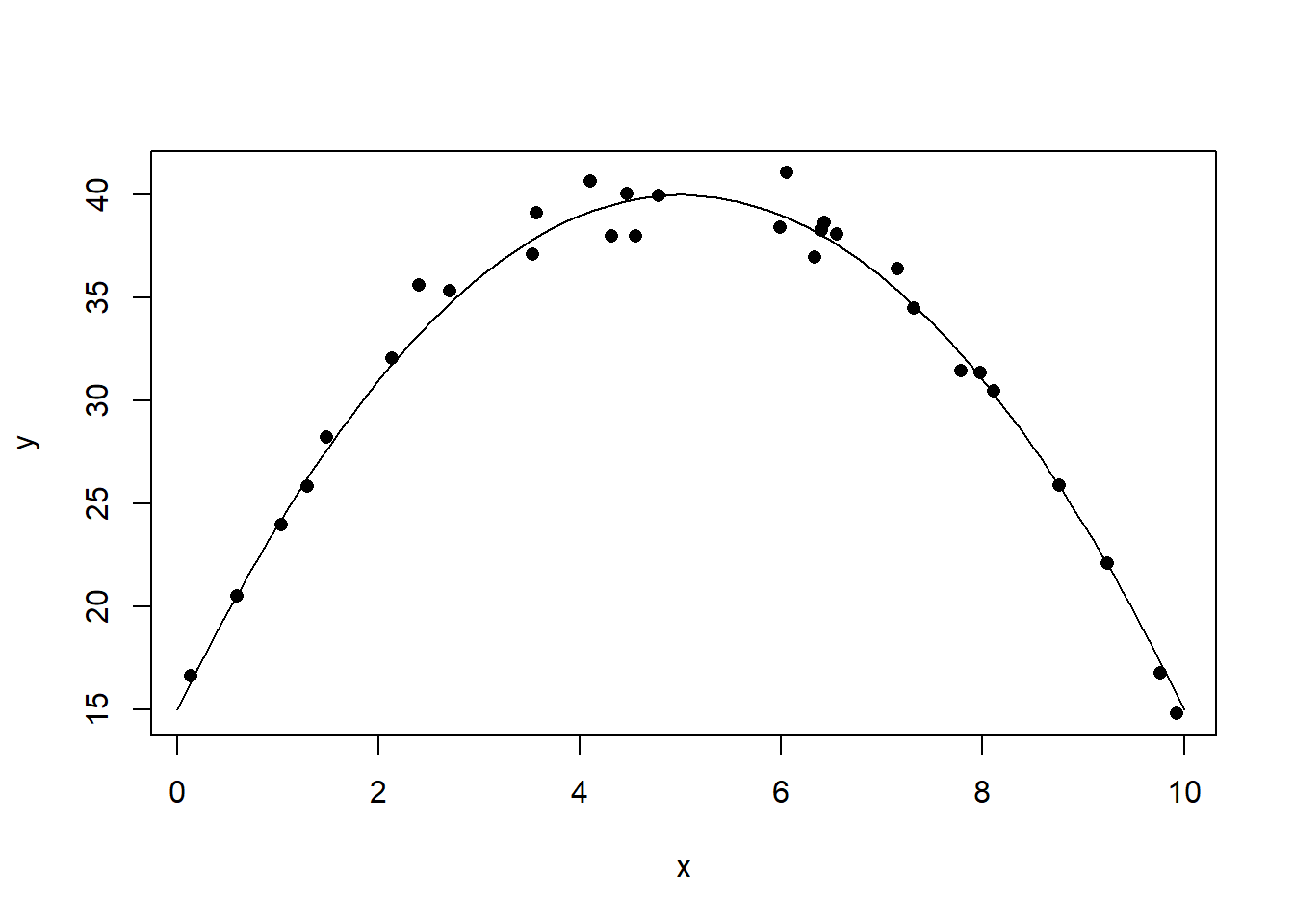
图32.6: 曲线相关数据的相关系数例2
## [1] -0.042684x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40*exp(-x/2) + rnorm(30)
yy <- 40*exp(-xx/2)
plot(x, y, pch=16)
lines(xx, yy)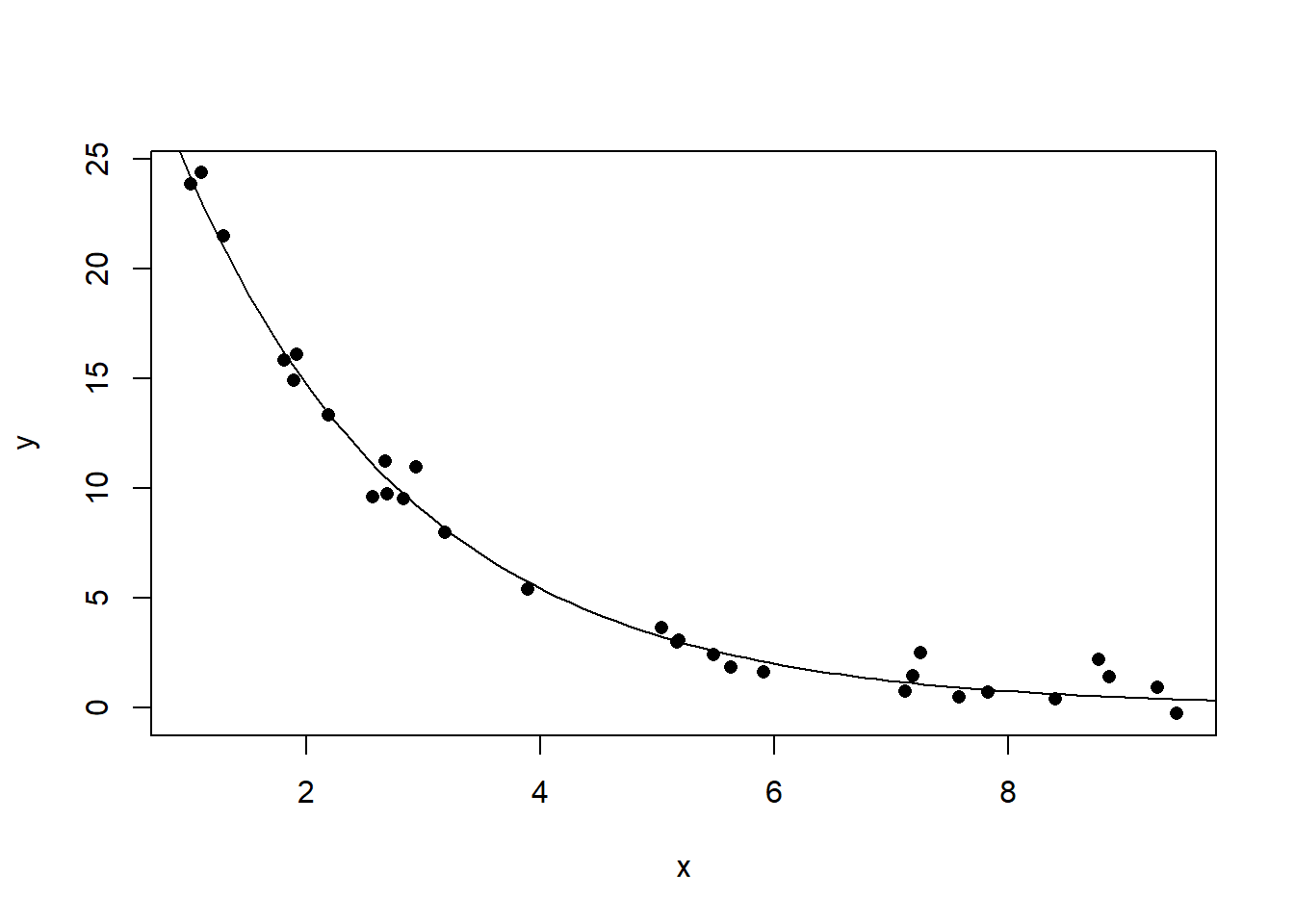
图32.7: 曲线相关数据的相关系数例3
## [1] -0.884111732.1.2 相关与因果
相关系数是从数据中得到的\(x\)和\(y\)两个变量关系的一种描述, 不能直接引申为因果关系。
例如,增加身高,不一定增长体重。
实际中有许多错误理解相关与因果性的例子。 例如:研究发现喝咖啡的人群比不喝咖啡的人群心脏病发病率高。 于是断言喝咖啡导致心脏病危险增加。 进一步研究更多的因素发现, 喝咖啡放糖很多的人心脏病发病率才增高了。
32.1.3 相关系数大小
- 相关系数绝对值在0.8以上认为高度相关。
- 在0.5到0.8之间认为中度相关。
- 在0.3到0.5之间认为低度相关。
- 在0.3以下认为不相关或相关性很弱以至于没有实际价值。
- 当然,在特别重要的问题中, 只要经过检验显著不等于零的相关都认为是有意义的。
32.1.4 相关系数的检验
相关系数\(r\)是总体相关系数\(\rho\)的估计。 \[H_0: \rho=0 \longleftrightarrow H_a: \rho\neq 0\] 检验统计量 \[t = \frac{r \sqrt{n-2}}{\sqrt{1 - r^2}}\] 当总体\((X, Y)\)服从二元正态分布且\(H_0: \rho=0\)成立时, \(t\)服从\(t(n-2)\)分布。 设\(t\)统计量值为\(t_0\),p值为 \[P(|t(n-2)| > |t_0|)\]
在R中用cor.test(x,y)计算检验。
例如:
##
## Pearson's product-moment correlation
##
## data: d.class$height and d.class$weight
## t = 7.5549, df = 17, p-value = 7.887e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7044314 0.9523101
## sample estimates:
## cor
## 0.8777852得身高与体重的相关系数为0.88,检验的p值为7.887e-07,
95%置信区间为\([0.70, 0.95]\)。
再例如:
##
## Pearson's product-moment correlation
##
## data: x and y
## t = 0.93076, df = 28, p-value = 0.3599
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.1994815 0.5021658
## sample estimates:
## cor
## 0.1732378得x与y的样本相关系数为0.17, p值为0.36,不显著。
32.1.5 相关阵
如果x是一个仅包含数值型列的数据框,
则cor(x)计算样本相关系数矩阵;
var(x)计算样本协方差阵。
corrgram::corrgram()可以绘制相关系数矩阵的图形,
用颜色和阴影浓度代表相关系数正负和绝对值大小,
用饼图中阴影部分大小代表相关系数绝对值大小。
如:
## Registered S3 method overwritten by 'seriation':
## method from
## reorder.hclust gcluscorrgram(
baseball[,c("Assists","Atbat","Errors","Hits","Homer","logSal",
"Putouts","RBI","Runs","Walks","Years")],
order=TRUE, main="Baseball data PC2/PC1 order",
lower.panel=panel.shade, upper.panel=panel.pie)
图32.8: 相关阵图形
其中选项order=TRUE重排各列的次序使得较接近的列排列在相邻位置。
32.2 一元回归分析
32.2.1 模型
考虑两个变量\(Y\)与\(X\)的关系,希望用\(X\)值的变化解释\(Y\)值的变化。 \(X\)称为自变量(independent variable),\(Y\)称为因变量(response variable)。
假设模型 \[\begin{aligned} Y = a + b X + \varepsilon, \quad \varepsilon \sim \text{N}(0,\sigma^2) \end{aligned} \]
设观测值为\((X_i, Y_i), i=1,2,\dots,n\),假设观测值满足上模型。 即 \[\begin{aligned} Y_i = a + b X_i + \varepsilon_i, \quad \varepsilon_i \text{ iid }\sim \text{N}(0,\sigma^2) \end{aligned} \]
32.2.2 最小二乘法
直观上看,要找最优的直线\(y=a+bx\)使得直线与观测到的点最接近。 例如:
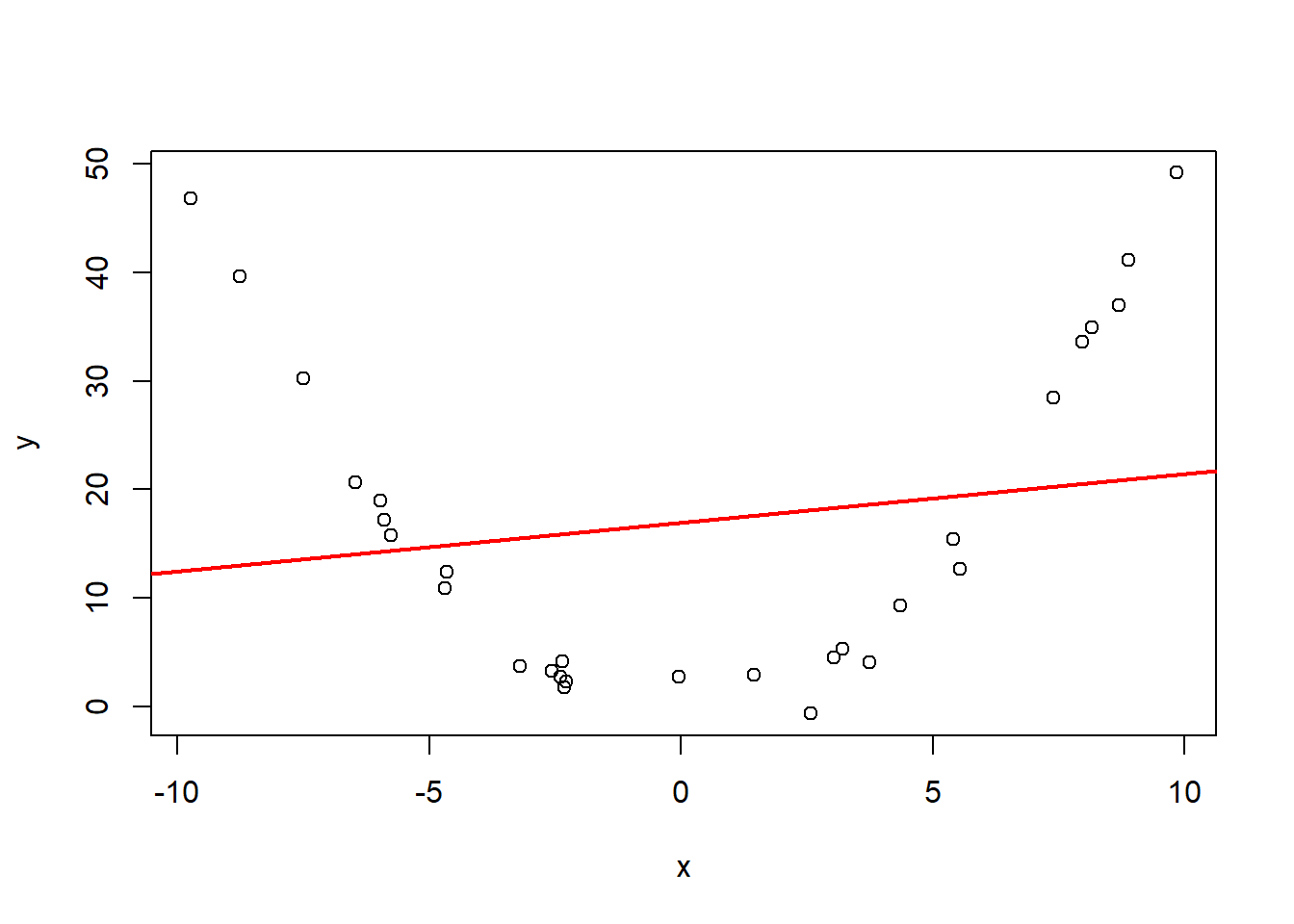
图32.9: 一元线性回归最小二乘估计
\(a,b\)的解用最小二乘法得到:
\[\min_{a,b} \sum_{i=1}^n \left( y_i - a - b x_i \right)^2\]
最小二乘解表达式为
\[\begin{aligned} \hat b =& \frac{\sum_i (x_i - \bar x)(y_i - \bar y)} {\sum_i (x_i - \bar x)^2} = r_{xy} \frac{S_y}{S_x} \\ \hat a =& \bar y - \hat b \bar x \end{aligned}\] 其中\(r_{xy}\)为\(X\)与\(Y\)的样本相关系数, \(S_x\)与\(S_y\)分别为\(X\)和\(Y\)的样本标准差。
随机误差方差\(\sigma^2\)的估计取为
\[ \hat\sigma^2 = \frac{1}{n-2}\sum_i (y_i - \hat a - \hat b x_i)^2 \]
标准误差: 为衡量\(\hat a\)和\(\hat b\)的估计精度, 计算\(\text{SE}(\hat a)\)和\(\text{SE}(\hat b)\)。
估计结果:
拟合值(预测值) \[\hat y_i = \hat a + \hat b x_i, \quad i=1,2,\dots,n\]
残差 \[e_i = y_i - \hat y_i, \quad i=1,2,\dots,n\]
\(\text{SSE}=\sum_i e_i^2\) 称为残差平方和,残差平方和小则拟合优。
32.2.3 回归有效性
32.2.3.1 拟合优度指标
按照最小二乘估计公式,只要\(x_1, x_2, \dots, x_n\)不全相等, 不论\(x, y\)之间有没有相关关系, 都能计算出参数估计值。 得到的回归直线与观测数据的散点之间的接近程度代表了回归结果的优劣。
残差平方和 \[\text{SSE}=\sum_{i=1}^n (y_i - \hat a - \hat b x_i)^2\] 残差平方和越小, 说明回归直线与观测数据点吻合得越好。
\(y\)是因变量, 因变量的数据的离差平方和 \[\text{SST}=\sum_{i=1}^n (y_i - \bar y)^2\] 代表了因变量的未知变动大小, 需要对这样的变动用自变量进行解释, 称SST为总平方和。
可以证明如下平方和分解公式: \[\text{SST} = \text{SSR} + \text{SSE}\] 其中SSR称为回归平方和。
令\(\hat y_i = \hat\beta_0 + \hat\beta_1 x_i\)称为第\(i\)个拟合值, 回归平方和为 \[\text{SSR}=\sum_{i=1}^n (\hat y_i - \bar y)^2 = \hat b^2 \sum_{i=1}^n (x_i - \bar x)^2 \]
在总平方和中, 回归平方和是能够用回归斜率与自变量的变动解释的部分, 残差平方和是自变量不能解释的变动。 分解中,回归平方和越大,误差平方和越小, 拟合越好。 令 \[R^2 = \frac{\text{SSR}}{\text{SST}} = 1 - \frac{\text{SSE}}{\text{SST}}\] 称为回归的复相关系数,或判定系数。
\(0 \leq R^2 \leq 1\)。判定系数越大,回归拟合越好。 \(R^2=1\)时,观测点完全落在一条直线上面。 一元回归中\(R^2\)是\(x\)和\(y\)的样本相关系数的平方。 在多元回归时只能用复相关系数。
估计误差项方差\(\sigma^2\)为 \[ \hat\sigma^2 = \frac{1}{n-2}\sum_{i=1}^n (y_i - \hat a - \hat b x_i)^2 = \frac{1}{n-2} \text{SSE} \]
\(\hat\sigma\)是\(\sigma\)的估计, R的回归结果中显示为“residual standard error”(残差标准误差)。 \(\hat\sigma\)是残差\(e_i = y_i - \hat y_i\)的标准差的一个粗略估计。
32.2.3.2 线性关系显著性检验
当\(b=0\)时,模型退化为\(Y = a + \varepsilon\),\(X\)不出现在模型中, 说明\(Y\)与\(X\)不相关。检验 \[ H_0: b=0 \longleftrightarrow H_\text{a}: b \neq 0 \]
取统计量 \[F = \frac{\text{SSR}}{\text{SSE}/(n-2)}\] 检验p值为\(P(F(1, n-2) > c)\)(设\(c\)为\(F\)统计量的值)。 取检验水平\(\alpha\), p值小于等于\(\alpha\)时拒绝\(H_0\), 认为\(y\)与\(x\)有显著的线性相关关系, 否则认为\(y\)与\(x\)没有显著的线性相关关系。
也可以使用t统计量 \[t = \frac{\hat b}{\text{SE}_{\hat b}}\] 其中 \[ \text{SE}_{\hat b} = \hat\sigma / \sqrt{\sum_{i=1}^n (x_i - \bar x)^2} \] 设t统计量的值为\(c\), 检验p值为\(P(|t(n-2)| > |c|)\)。
32.2.4 R程序
设数据保存在数据框d中,变量名为y和x,用R的lm()函数计算回归,如:
set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
y <- 20 + 0.5*x + rnorm(nsamp,0,0.5)
d <- data.frame(x=x, y=y)
lm1 <- lm(y ~ x, data=d); lm1##
## Call:
## lm(formula = y ~ x, data = d)
##
## Coefficients:
## (Intercept) x
## 20.0388 0.4988结果只有回归系数。需要用summary()显示较详细的结果。如
##
## Call:
## lm(formula = y ~ x, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.03030 -0.16436 -0.05741 0.29511 0.64046
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 20.03883 0.07226 277.3 <2e-16 ***
## x 0.49876 0.01244 40.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.3956 on 28 degrees of freedom
## Multiple R-squared: 0.9829, Adjusted R-squared: 0.9823
## F-statistic: 1608 on 1 and 28 DF, p-value: < 2.2e-16结果中\(H_0: b=0\)的检验结果p值为\(<2e-16\)。
又如对d.class数据集,建立体重对身高的回归方程:
##
## Call:
## lm(formula = weight ~ height, data = d.class)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.6807 -6.0642 0.5115 9.2846 18.3698
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -143.0269 32.2746 -4.432 0.000366 ***
## height 3.8990 0.5161 7.555 7.89e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.23 on 17 degrees of freedom
## Multiple R-squared: 0.7705, Adjusted R-squared: 0.757
## F-statistic: 57.08 on 1 and 17 DF, p-value: 7.887e-07身高对体重的影响是显著的(p值7.89e-7)。
32.2.5 回归诊断
除了系数的显著性检验以外, 对误差项是否符合回归模型假定中的独立性、方差齐性、正态性等, 可以利用回归残差进行一系列的回归诊断。 还可以计算一些异常值、强影响点的诊断。
对\(n\)组观测值,回归模型为 \[ y_i = a + b x_i + \varepsilon_i \] 拟合值为 \[ \hat y_i = \hat a + \hat b x_i \] 残差(residual)为 \[e_i = y_i - \hat y_i\]
残差相当于模型中的随机误差, 但仅在模型假定成立时才是随机误差的合理估计。 所以残差能够反映违反模型假定的情况。
\(e_i\)有量纲,不好比较大小。 定义标准化残差(内部学生化残差): \[ r_i = \frac{e_i}{S_e\sqrt{1 - \frac{1}{n} - \frac{(x_i - \bar x)^2}{\sum_{k=1}^n (x_k - \bar x)^2}}} \] 样本量较大时标准化残差近似服从标准正态分布, 于是取值于\([-2,2]\)范围外的点是可疑的离群点。
R中用residuals()从回归结果计算残差,
用rstandard()从回归结果计算标准化残差。
R中plot(lmres)(lmres为回归结果变量)可以做简单回归诊断。
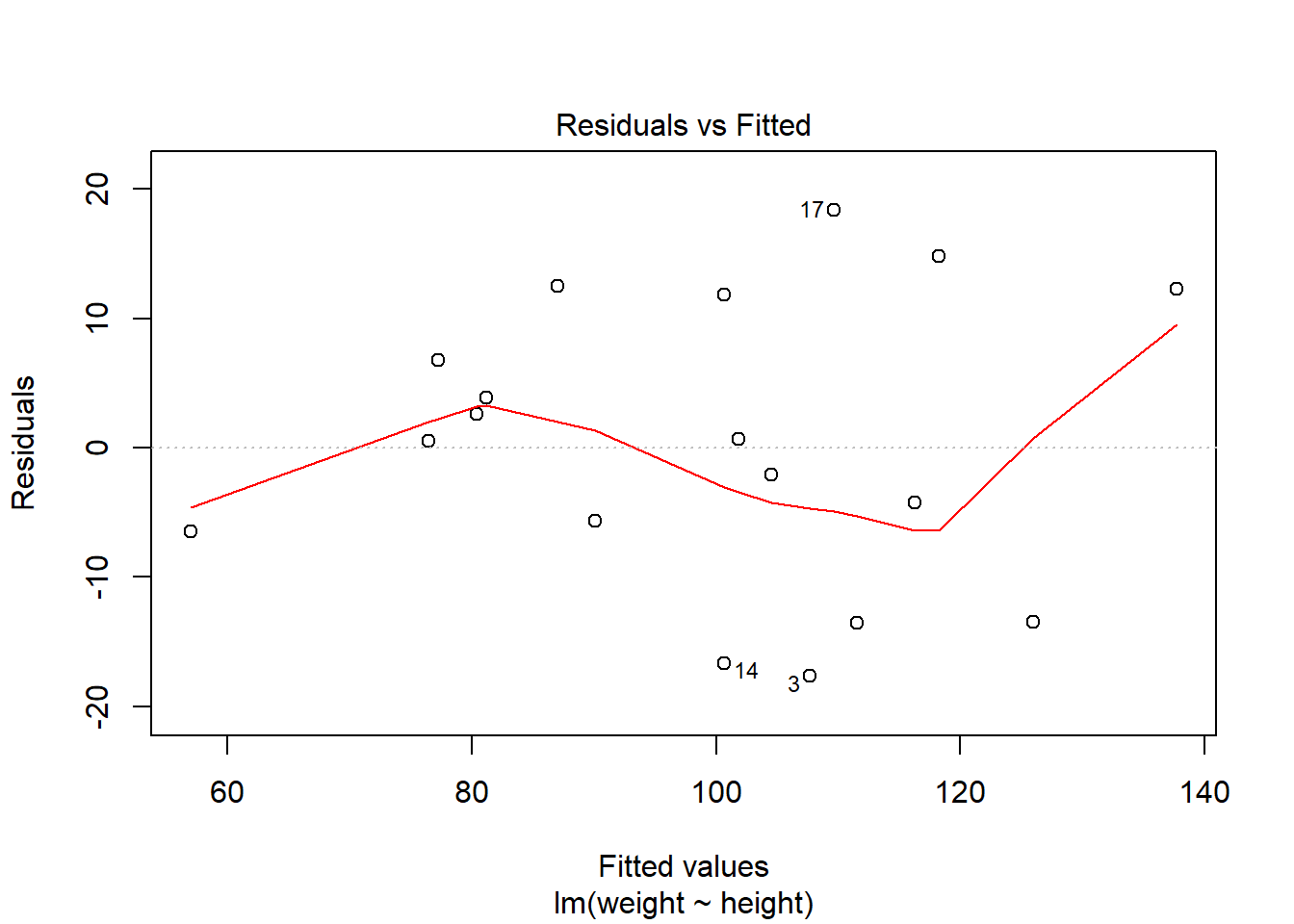
第一个图是残差对预测值散点图, 散点应该随机在0线上下波动,不应该有曲线模式、分散程度增大模式、 特别突出的离群点等情况。
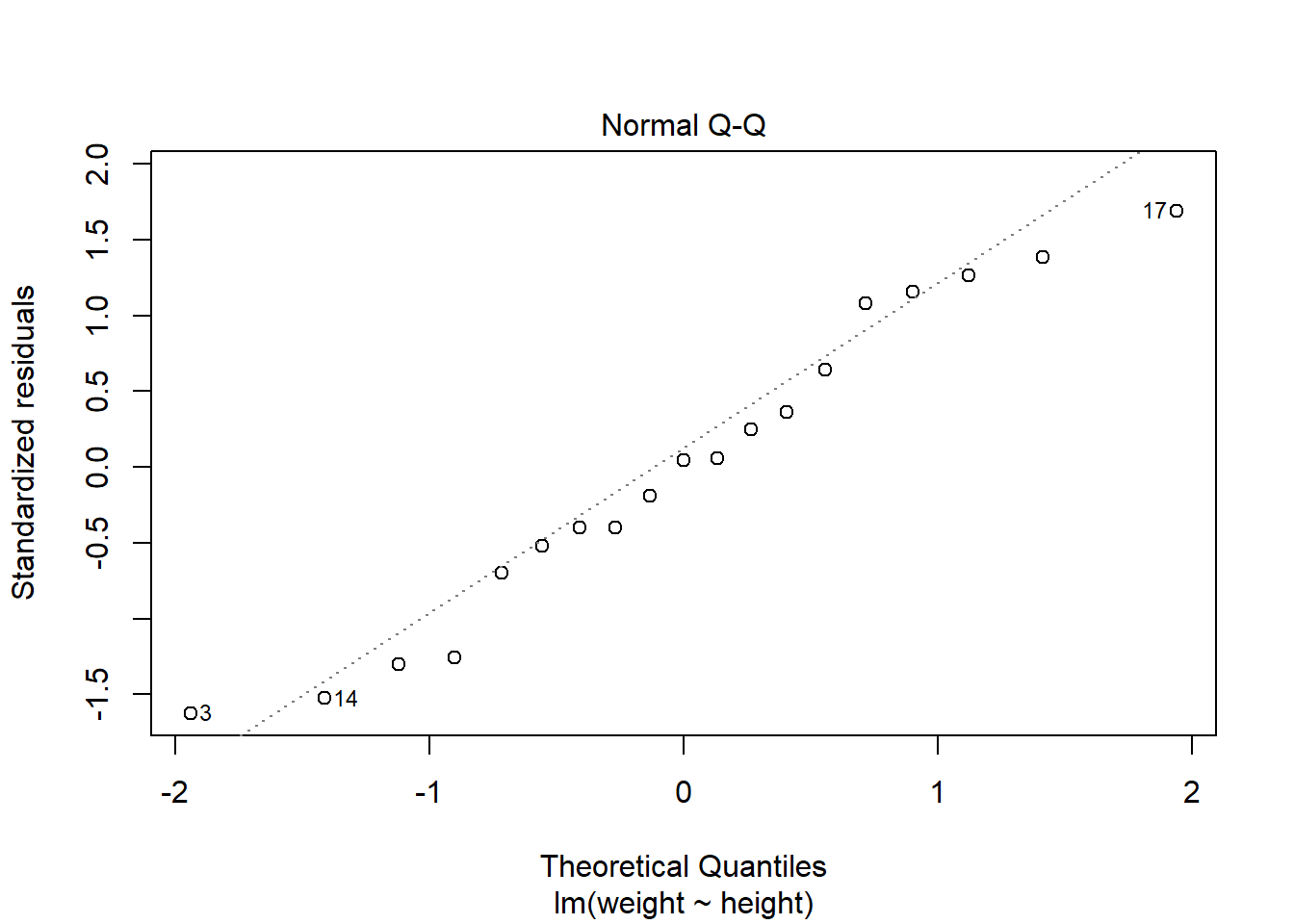
第二个图是残差的正态QQ图, 散点接近于直线时可以认为模型误差项的正态分布假定是合理的。
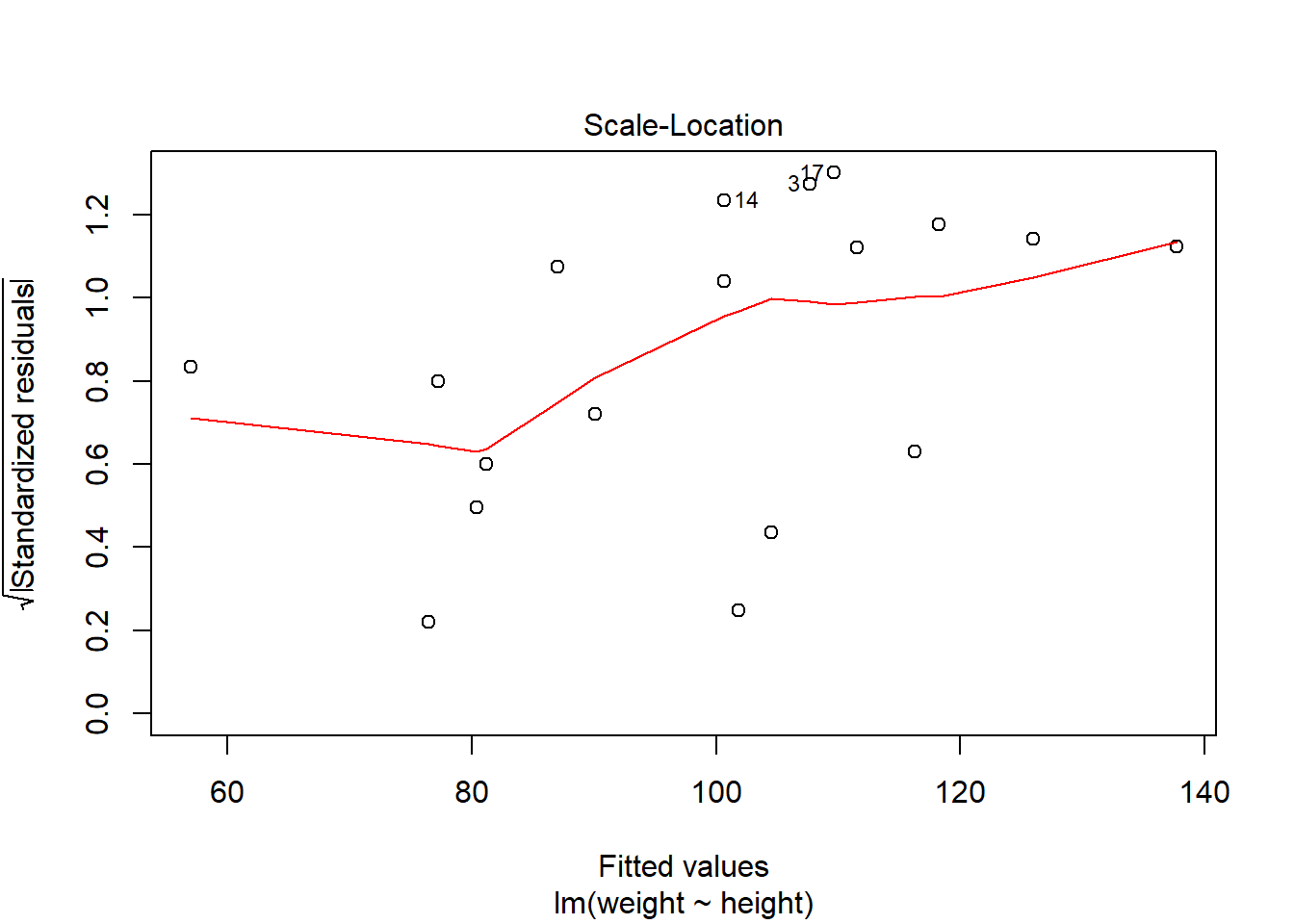
第三个图是误差大小(标准化残差绝对值的平方根)对拟合值的图形, 可以判断方差齐性假设(方差\(\sigma^2\)不变)。
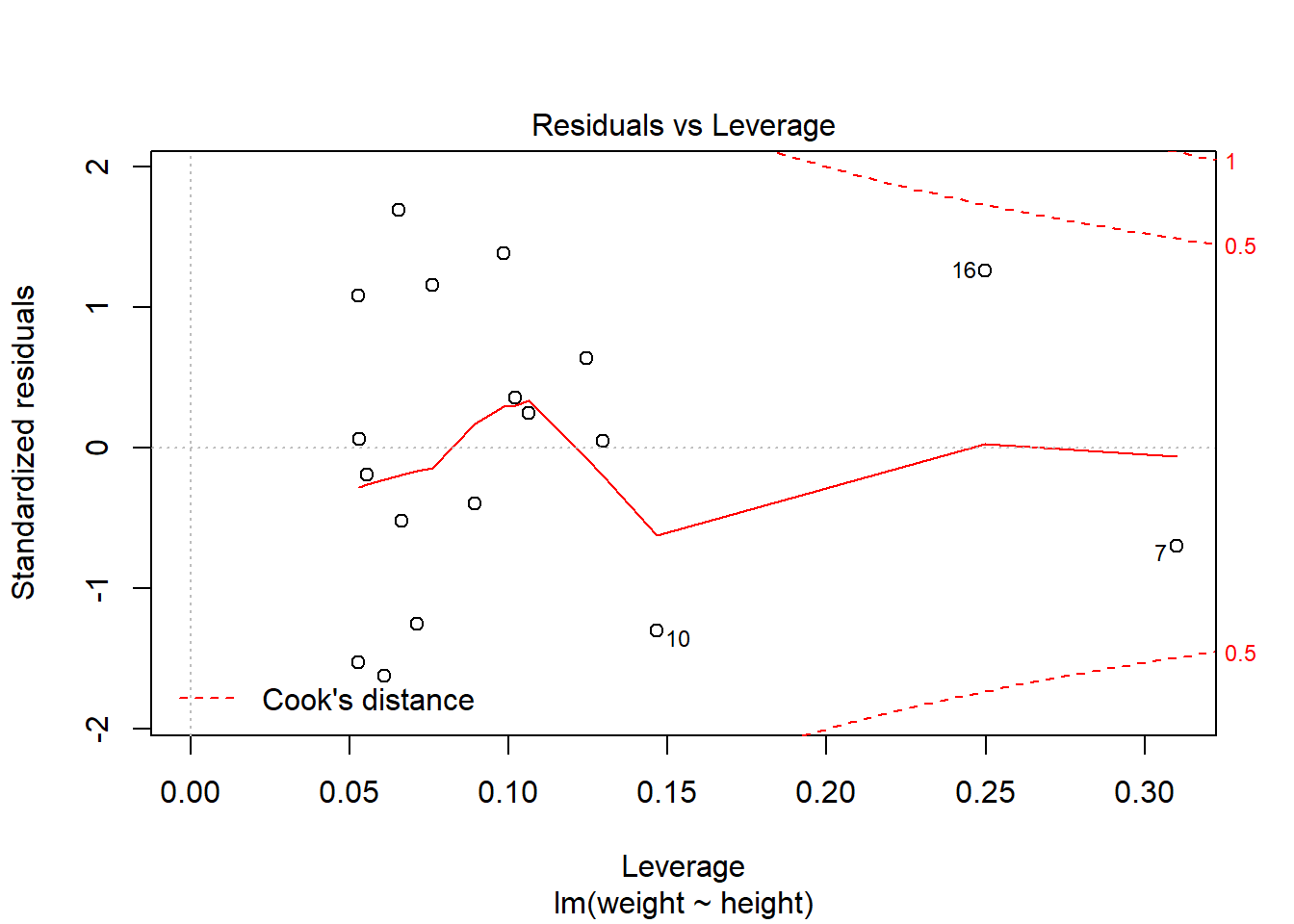
第四个图是残差对杠杆量图,并叠加了Cook距离等值线。 杠杆量代表了回归自变量对结果的影响大小, 超过\(4/n\)的值是需要重视的。 Cook距离考察删去第\(i\)个观测对回归结果的影响。
## [,1] [,2]
## 1 6.7317083 0.64090788
## 2 -13.5797581 -1.25514370
## 3 -17.6807278 -1.62510342
## 4 0.5115143 0.04884012
## 5 -5.6350916 -0.51945382
## 6 -4.2585944 -0.39749776
## 7 -6.4933343 -0.69635607
## 8 11.8375266 1.08337723
## 9 0.6678176 0.06113186
## 10 -13.5061701 -1.30222590
## 11 -2.0615036 -0.18894975
## 12 14.7918904 1.38780152
## 13 2.6124840 0.24615612
## 14 -16.6624734 -1.52495912
## 15 12.4841326 1.15698074
## 16 12.2967391 1.26478834
## 17 18.3697570 1.69265472
## 18 3.8326780 0.36028625
## 19 -4.2585944 -0.39749776可以用\(e_i\)或\(r_i\)作为纵坐标, \(x_i\)或者\(\hat y_i\)作为横坐标, 作残差图。
下面给出残差图的几种常见的缺陷:
非线性:
set.seed(1)
x <- runif(30, 0, 10)
xx <- seq(0, 10, length.out = 100)
y <- 40 - (x-7)^2 + rnorm(30)
yy <- 40 - (xx-7)^2
lms1 <- lm(y ~ x)
opar <- par(mfrow=c(1,2))
plot(x, y, pch=16, main="数据和真实模型")
lines(xx, yy)
plot(x, rstandard(lms1), main="使用线性回归的残差")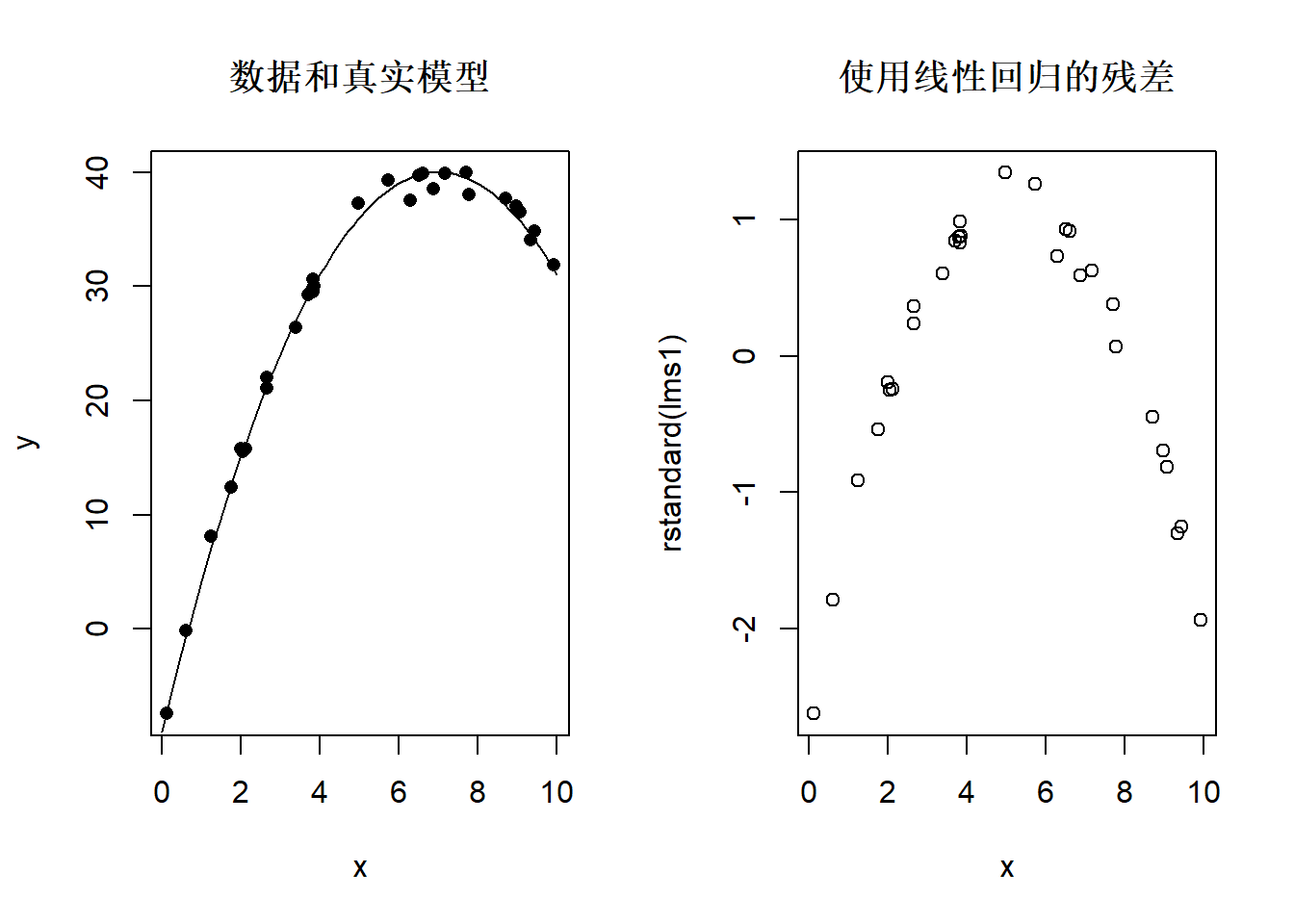
图32.10: 残差中非线性模式
异方差:
x <- sort(runif(30, 0, 10))
y <- 10 + 2*x + rnorm(30)*(seq(30)/10)
lms2 <- lm(y ~ x)
opar <- par(mfrow=c(1,2))
plot(x, y, pch=16, main="数据和真实模型")
abline(a=10, b=2)
plot(x, rstandard(lms2), main="线性模型的残差")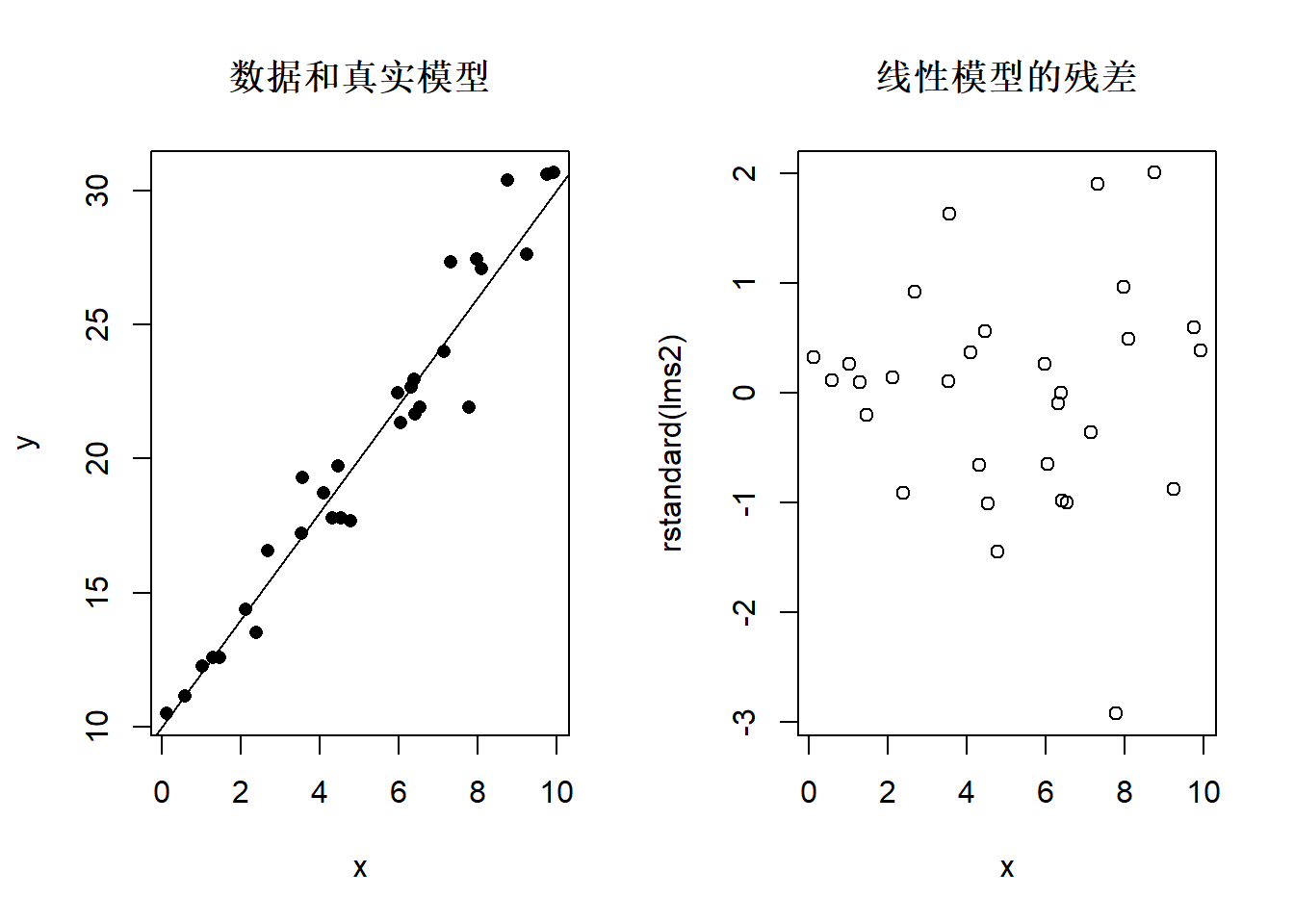
序列自相关:
当数据随时间变化时,还需要考虑前后是否有序列自相关。 自相关残差图形例子:
ar1 <- arima.sim(list(ar=c(0.5)), n=30)
plot(1:30, ar1[], type="l", xlab="time", ylab="residual",
main="有序列自相关的残差图形")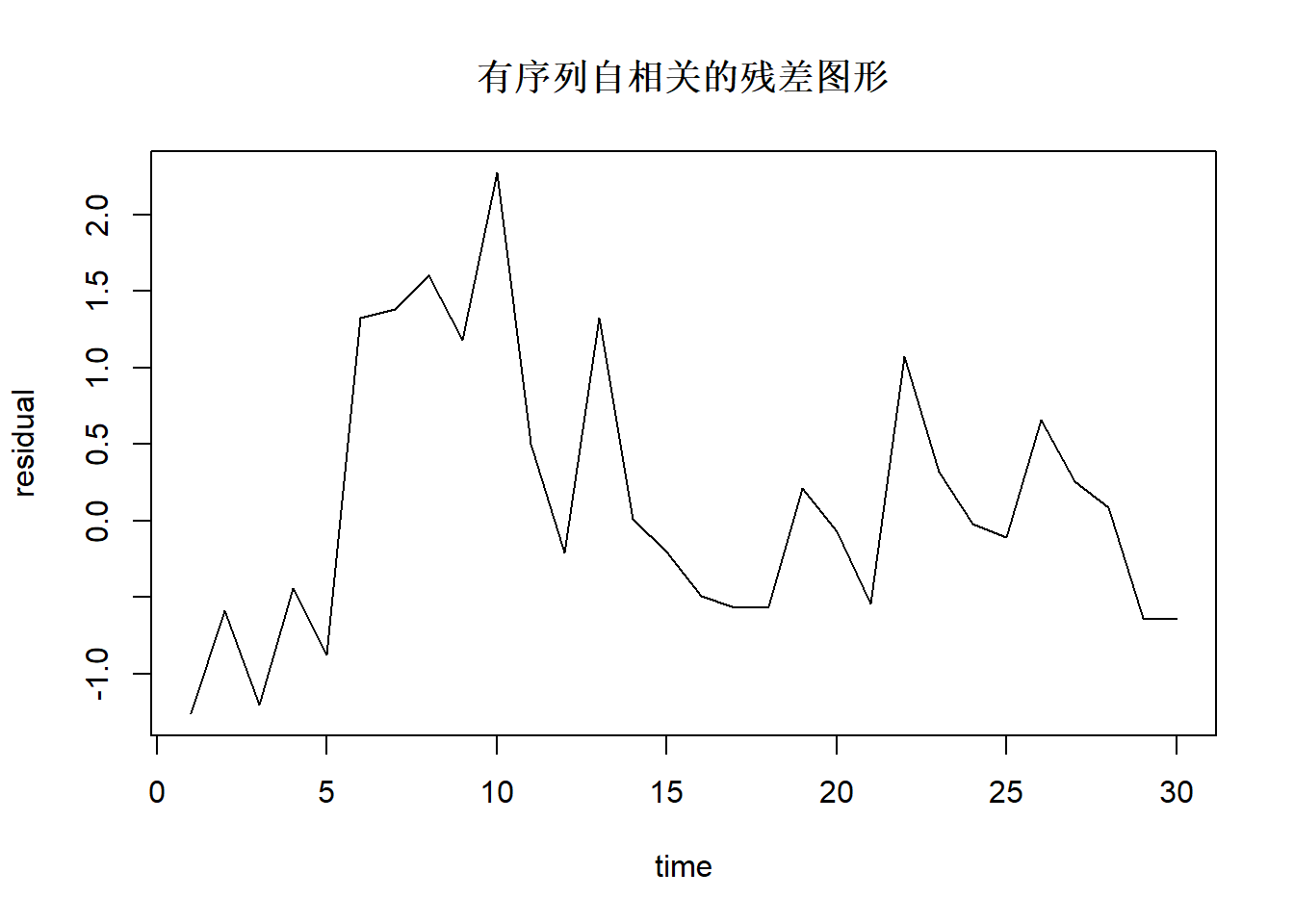
图中横坐标是观测序号。
car::ncvTest()检验方差齐性。零假设是方差齐性成立。
如
## Non-constant Variance Score Test
## Variance formula: ~ fitted.values
## Chisquare = 1.664307, Df = 1, p = 0.19702用Durbin-Watson检验(DW检验)可以检验残差中是否有序列自相关,
零假设是没有序列自相关。
R中用car::durbinWatsonTest()检验。
序列自相关检验仅当数据中数据是延时间等间隔记录时有意义。
如
## lag Autocorrelation D-W Statistic p-value
## 1 0.1959139 1.57293 0.21
## Alternative hypothesis: rho != 0也可以对回归残差绘制ACF图, 如果除了横坐标0之外都落在两条水平界限内则认为没有序列自相关, 如果有明显超出界限的就认为有序列自相关。 如
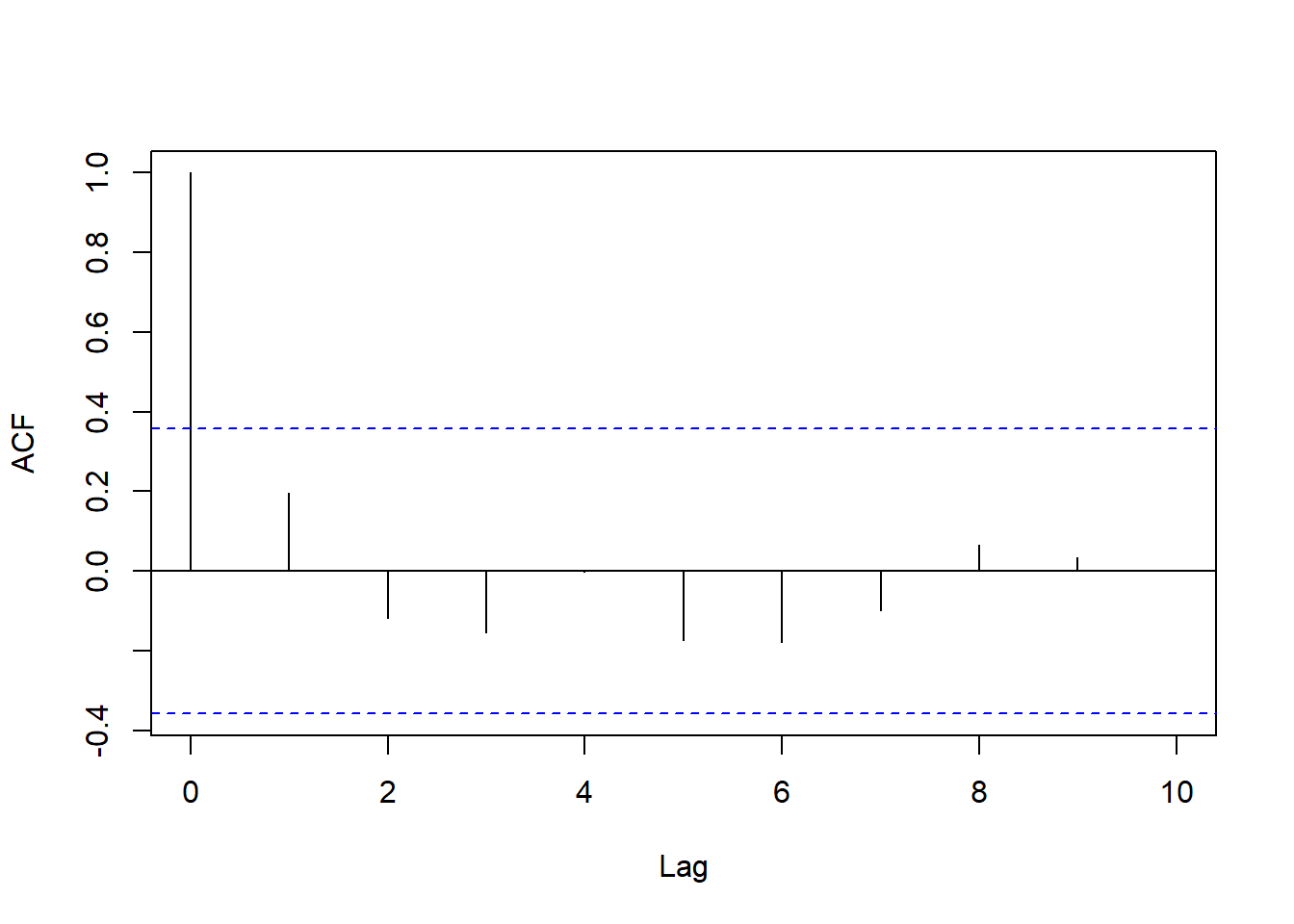
32.2.6 预测区间
设\(X\)取\(x_0\),\(Y\)的预测值为\(\hat y_0 = \hat a + \hat b x_0\)。
置信水平为\(1-\alpha\)的预测区间为
\[\hat y_0 \pm \lambda \hat\sigma
\sqrt{1 + \frac{1}{n}
+ \frac{(\bar x - x_0)^2}{\sum_i (x_i - \bar x)^2}}
\]
其含义是\(P(y_0 \in \text{预测区间}) = 1 - \alpha\)。
\(\lambda\)是标准正态分布双侧\(\alpha\)分位数qnorm(1 - alpha/2)。
用predict(lmres)得到\(\hat y_i, i=1,\dots,n\)的值,
lmres表示回归结果变量。
用predict(lmres, interval="prediction")
同时得到预测的置信区间,
需要的话加入level=选项设定置信度。
回归的置信区间有两种, 上述的区间是“预测区间”(CLI), 使得\(P(y_0 \in \text{预测区间}) = 1 - \alpha\); 另一种区间称为均值的置信区间(CLM), 使得\(P(Ey_0 \in \text{均值置信区间}) = 1 - \alpha\)。
32.2.7 控制
如果需要把\(Y\)的值控制在\([y_l, y_u]\)范围内,问如何控制\(X\)的范围, 可以求解\(x_0\)的范围使上面的置信区间包含在\([y_l, y_u]\)内。
近似地可以解不等式
\[\begin{aligned}
\hat a + \hat b x_0 - z_{1-\frac{\alpha}{2}} \hat \sigma \geq & y_l \\
\hat a + \hat b x_0 + z_{1-\frac{\alpha}{2}} \hat \sigma \leq & y_u
\end{aligned}\]
其中\(z_{1-\frac{\alpha}{2}}\)为标准正态分布双侧\(\alpha\)分位数
(用qnorm(1-alpha/2)计算)。
32.3 多元线性回归
建模步骤:
- 确定要研究的因变量,以及可能对因变量有影响并且数据可以获得的自变量集合
- 假定因变量\(y\)与\(p\)个自变量之间为线性相关关系,建立模型
- 对模型进行评估和检验
- 判断模型中是否存在多重共线性,如果存在,应进行处理
- 预测
- 残差分析
32.3.1 模型
模型 \[ y = \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p + \varepsilon \] 其中
- \(y\): 因变量,随机变量
- \(x_1, \dots, x_p\): 自变量,非随机
- \(\varepsilon\): 随机误差项,随机变量
- \(\beta_0\): 截距项
- \(\beta_j\): 对应于\(x_j\)的斜率项
- 模型表明因变量\(y\)近似等于自变量的线性组合
- \(E \varepsilon=0\), \(\text{Var}(\varepsilon)=\sigma^2\)
对\(n\)组观测数据, 有 \[ y_i = \beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip} + \varepsilon_i, \quad i=1,2,\dots, n \] 对其中的随机误差项\(\varepsilon_i\), \(i=1,2,\dots,n\),假定:
- 期望为零,服从正态分布;
- 方差齐性: 方差为\(\sigma^2\)与自变量值无关;
- 相互独立。
总之,\(\varepsilon_1, \varepsilon_2, \dots, \varepsilon_n\) 相互独立,服从\(\text{N}(0, \sigma^2)\)分布。
数据格式如: \[ \left(\begin{array}{cccc|c} x_1 & x_2 & \cdots & x_p & y\\ \hline x_{11} & x_{12} & \cdots & x_{1p} & y_1 \\ x_{21} & x_{22} & \cdots & x_{2p} & y_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} & y_n \end{array}\right) \] R中回归数据放在一个数据框中,有一列\(y\)和\(p\)列自变量。
根据模型有 \[ Ey = \beta_0 + \beta_1 x_1 + \dots + \beta_p x_p \]
32.3.2 参数估计
未知的参数有回归系数\(\beta_0, \beta_1, \dots, \beta_p, \sigma^2\), 另外误差项也是未知的。
模型估计仍使用最小二乘法,得到系数估计 \(\hat\beta_0, \hat\beta_1, \dots, \hat\beta_p\) 及误差方差估计\(\hat\sigma^2\)。 得到估计的多元线性回归方程: \[ \hat y = \hat\beta_0 + \hat\beta_1 x_1 + \dots + \hat\beta_p x_p \]
对第\(i\)组观测值,将自变量值代入估计的回归方程中得拟合值 \[ \hat y_i = \hat\beta_0 + \hat\beta_1 x_{i1} + \dots + \hat\beta_p x_{ip} \] \(e_i = y_i - \hat y_i\)称为残差。 回归参数估计,用残差最小作为目标,令 \[ Q = \sum_{i=1}^n \left[ y_i - (\beta_0 + \beta_1 x_{i1} + \dots + \beta_p x_{ip}) \right]^2 \] 取使得\(Q\)达到最小的\((\beta_0, \beta_1, \dots, \beta_p)\)作为参数估计, 称为最小二乘估计,记为\((\hat\beta_0, \hat\beta_1, \dots, \hat\beta_p)\)。 称得到的最小值为SSE,\(\sigma^2\)的估计为 \[ \hat\sigma^2 = \frac{1}{n-p-1} \text{SSE} = \frac{1}{n-p-1} \sum_{i=1}^n e_i^2 \]
32.3.3 R的多元回归程序
在R中用lm(y ~ x1 + x2 + x3, data=d)这样的程序来做多元回归,
数据集为d, 自变量为x1,x2,x3三列。
32.3.3.1 例:体重对身高和年龄的回归
考虑d.class数据集中体重对身高和年龄的回归:
##
## Call:
## lm(formula = weight ~ height + age, data = d.class)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.962 -6.010 -0.067 7.553 20.796
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -141.2238 33.3831 -4.230 0.000637 ***
## height 3.5970 0.9055 3.973 0.001093 **
## age 1.2784 3.1101 0.411 0.686492
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.51 on 16 degrees of freedom
## Multiple R-squared: 0.7729, Adjusted R-squared: 0.7445
## F-statistic: 27.23 on 2 and 16 DF, p-value: 7.074e-06得到的回归模型可以写成 \[ \widehat{\text{weight}} = -141.2 + 3.597 \times \text{height} + 1.278 \times \text{age} \] 其中身高的系数3.597表示, 如果两个学生年龄相同, 则身高增加1个单位(这里是英寸), 体重平均增加3.597个单位(这里是磅)。 注意在仅有身高作为自变量时, 系数为3.899。 年龄的系数1.278也类似解释, 在两个学生身高相同时, 如果一个学生年龄大1岁, 则此学生的体重平均多1.278个单位。
32.3.3.2 例:驾驶员行驶时间的模型
Butler Trucking Company是一个短途货运公司。 老板想研究每个驾驶员每天的行驶时间的影响因素。 随机抽取了10名驾驶员一天的数据。考虑行驶里程(Miles)对行驶时间的影响。
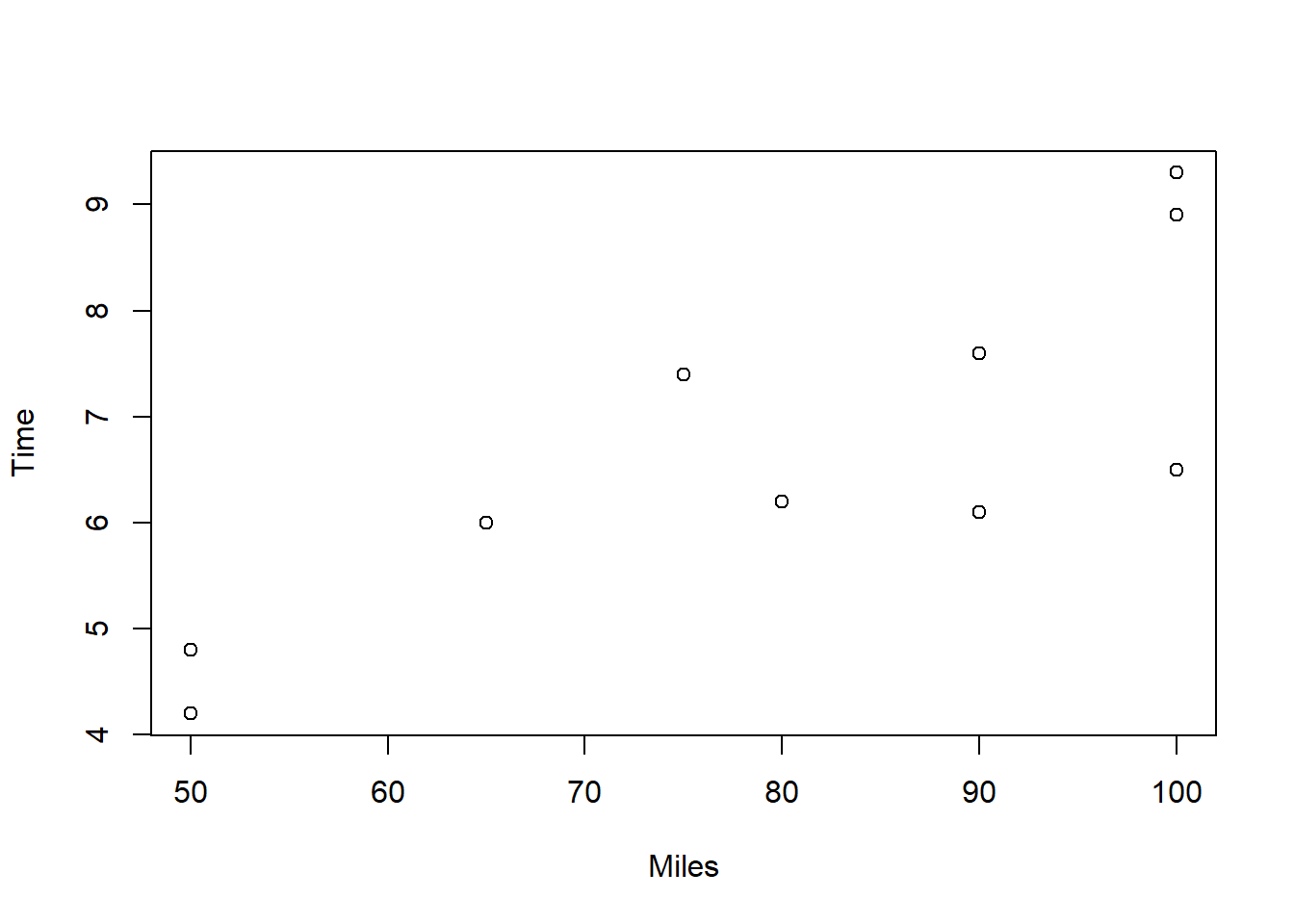
从散点图看,行驶里程与行驶时间有线性相关关系。 作一元线性回归:
##
## Call:
## lm(formula = Time ~ Miles, data = Butler)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.5565 -0.4913 0.1783 0.7120 1.2435
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.27391 1.40074 0.909 0.38969
## Miles 0.06783 0.01706 3.977 0.00408 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.002 on 8 degrees of freedom
## Multiple R-squared: 0.6641, Adjusted R-squared: 0.6221
## F-statistic: 15.81 on 1 and 8 DF, p-value: 0.00408这里Miles的系数解释为:行驶里程增加1英里,时间平均增加0.068小时。 老板想进一步改进对行驶时间的预测, 增加“派送地点数”(Deliveries)作为第二个自变量。 作多元回归:
##
## Call:
## lm(formula = Time ~ Miles + Deliveries, data = Butler)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.79875 -0.32477 0.06333 0.29739 0.91333
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.868701 0.951548 -0.913 0.391634
## Miles 0.061135 0.009888 6.182 0.000453 ***
## Deliveries 0.923425 0.221113 4.176 0.004157 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5731 on 7 degrees of freedom
## Multiple R-squared: 0.9038, Adjusted R-squared: 0.8763
## F-statistic: 32.88 on 2 and 7 DF, p-value: 0.0002762这里Miles的系数从一元回归时的0.068改成了0.061, 解释为:在派送地点数相同的条件下,行驶里程每增加1英里, 行驶时间平均增加0.061小时。
Deliveries的系数解释为:在行驶里程相同的条件下, 派送地点数每增加一个地点,行驶时间平均增加0.92小时。
32.3.4 模型的检验
32.3.4.1 复相关系数平方
将总平方和分解为: \[ \text{SST} = \text{SSR} + \text{SSE} \] 其中 - 总平方和 \[\text{SST} = \sum_{i=1}^n (y_i - \bar y)^2\] - 回归平方和 \[\text{SSR} = \sum_{i=1}^n (\hat y_i - \bar y)^2\] 是能够用回归系数和自变量的变量解释的因变量变化。 - 残差平方和 \[\text{SSE} = \sum_{i=1}^n (y_i - \hat y_i)^2\] 是回归模型不能解释的因变量变化。
回归平方和越大,残差平方和越小,回归拟合越好。 定义复相关系数平方(判定系数) \[ R^2 = \frac{\text{SSR}}{\text{SST}} = 1 - \frac{\text{SSE}}{\text{SST}} \] 则\(0 \leq R^2 \leq 1\)。 \(R^2\)越大,说明数据中的自变量拟合因变量值拟合越好。
但是,“拟合好”不是唯一标准。 仅考虑拟合好, 可能产生很复杂的仅对建模用数据有效但是对其它数据无效的模型, 这称为“过度拟合”。
定义调整的(修正的)复相关系数平方: \[ R^{*2} = 1 - (1-R^2)\frac{n-1}{n-p-1} \] 克服了\(R^2\)的部分缺点。
在体重与身高、年龄的模型结果中, \(R^2=0.7729\), \(R^{*2}=0.7445\)。
32.3.4.2 残差标准误差
模型中\(\varepsilon\)的方差\(\sigma^2\)的估计为\(\hat\sigma_e^2\), \[ \hat\sigma^2 = \frac{1}{n-p-1}\text{SSE} \]
\(\hat\sigma\)是随机误差的标准差\(\sigma\)的估计量, 称为“残差标准误差”(Residual standard error)。 这是残差\(e_i = y_i - \hat y_i\)的标准差的一个较粗略的近似估计。
在体重与身高、年龄的模型结果中, \(\hat\sigma=11.51\)。
32.3.4.3 线性关系检验
为了检验整个回归模型是否都无效,考虑假设检验: \[ H_0: \beta_1 = \dots = \beta_p = 0 \] 当\(H_0\)成立时模型退化成\(y=\beta_0 + \varepsilon\), \(y\)与\(x_1, x_2, \dots, x_p\)之间不再具有线性相关关系。
取统计量为 \[ F = \frac{\text{SSR}/p}{\text{SSE}/(n-p-1)} \] 在模型前提条件都满足且\(H_0\)成立时\(F\)服从\(F(p, n-p-1)\)分布。 计算右侧\(p\)值,给出检验结论。
当检验显著时,各斜率项不全为零。 结果不显著时,当前回归模型不能使用。
在体重与身高、年龄的模型结果中, \(F=27.23\),p值为\(7.074\times 10^{-6}\), 在0.05水平下显著, 模型有意义。
32.3.4.4 单个斜率项的显著性检验
为了检验某一个自变量\(X_j\)是否对因变量的解释有贡献 (在模型中已经包含了其它自变量的情况下),检验 \[H_0: \beta_j = 0\] 如果不拒绝\(H_0\), 相当于\(x_j\)可以不出现在模型中。 但是, 在多元线性回归中这不代表\(x_j\)与\(y\)之间没有线性相关, 可能是由于其它的自变量包含了\(x_j\)中的信息。
检验使用如下\(t\)统计量 \[ t = \frac{\hat\beta_j}{\text{SE}_{\hat\beta_j}} \] 在模型前提条件都满足且\(H_0\)成立时\(t\)服从\(t(n-p-1)\)分布。 给定检验水平\(\alpha\),计算双侧\(p\)值,做出检验结论。
对单个回归系数的检验,检验水平可取得略高,如0.10, 0.15。
在体重与身高、年龄的模型结果中, 身高的斜率项显著性p值为0.001, 在0.15水平下显著; 体重的斜率项显著性p值为0.686, 在0.15水平下不显著, 可考虑从模型中去掉体重变量。
32.3.5 回归自变量筛选
在19个学生的体重与身高、年龄的线性回归模型结果中, 发现关于年龄的系数为零的检验p值为0.686, 不显著, 说明在模型中已经包含身高的情况下, 年龄不提供对体重的额外信息。
但是如果体重对年龄单独建模的话,年龄的影响还是显著的:
##
## Call:
## lm(formula = weight ~ age, data = d.class)
##
## Residuals:
## Min 1Q Median 3Q Max
## -23.349 -7.609 -5.260 7.945 42.847
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -50.493 33.290 -1.517 0.147706
## age 11.304 2.485 4.548 0.000285 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.74 on 17 degrees of freedom
## Multiple R-squared: 0.5489, Adjusted R-squared: 0.5224
## F-statistic: 20.69 on 1 and 17 DF, p-value: 0.0002848模型中不显著的自变量应该逐一剔除。可以用
step函数进行逐步回归变量选择,如:
## Start: AIC=94.93
## weight ~ height + age + sex
##
## Df Sum of Sq RSS AIC
## - age 1 113.76 1957.8 94.067
## <none> 1844.0 94.930
## - sex 1 276.09 2120.1 95.581
## - height 1 1020.61 2864.6 101.299
##
## Step: AIC=94.07
## weight ~ height + sex
##
## Df Sum of Sq RSS AIC
## - sex 1 184.7 2142.5 93.780
## <none> 1957.8 94.067
## - height 1 5696.8 7654.6 117.974
##
## Step: AIC=93.78
## weight ~ height
##
## Df Sum of Sq RSS AIC
## <none> 2142.5 93.78
## - height 1 7193.2 9335.7 119.75##
## Call:
## lm(formula = weight ~ height, data = d.class)
##
## Residuals:
## Min 1Q Median 3Q Max
## -17.6807 -6.0642 0.5115 9.2846 18.3698
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -143.0269 32.2746 -4.432 0.000366 ***
## height 3.8990 0.5161 7.555 7.89e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.23 on 17 degrees of freedom
## Multiple R-squared: 0.7705, Adjusted R-squared: 0.757
## F-statistic: 57.08 on 1 and 17 DF, p-value: 7.887e-07考虑另一个例子数据。 在数据框Resturant中包含25个餐馆的一些信息,包括:
- \(y\), 营业额, 日均营业额(万元)
- \(x_1\), 居民数, 周边居民人数(万人)
- \(x_2\), 人均餐费, 用餐平均支出(元/人)
- \(x_3\), 月收入, 周边居民月平均收入(元)
- \(x_4\), 餐馆数, 周边餐馆数(个)
- \(x_5\), 距离, 距市中心距离(km)
对营业额进行回归建模研究。 变量间的相关系数图:
corrgram::corrgram(
Resturant, order=TRUE,
lower.panel=corrgram::panel.shade,
upper.panel = corrgram::panel.pie,
text.panel = corrgram::panel.txt)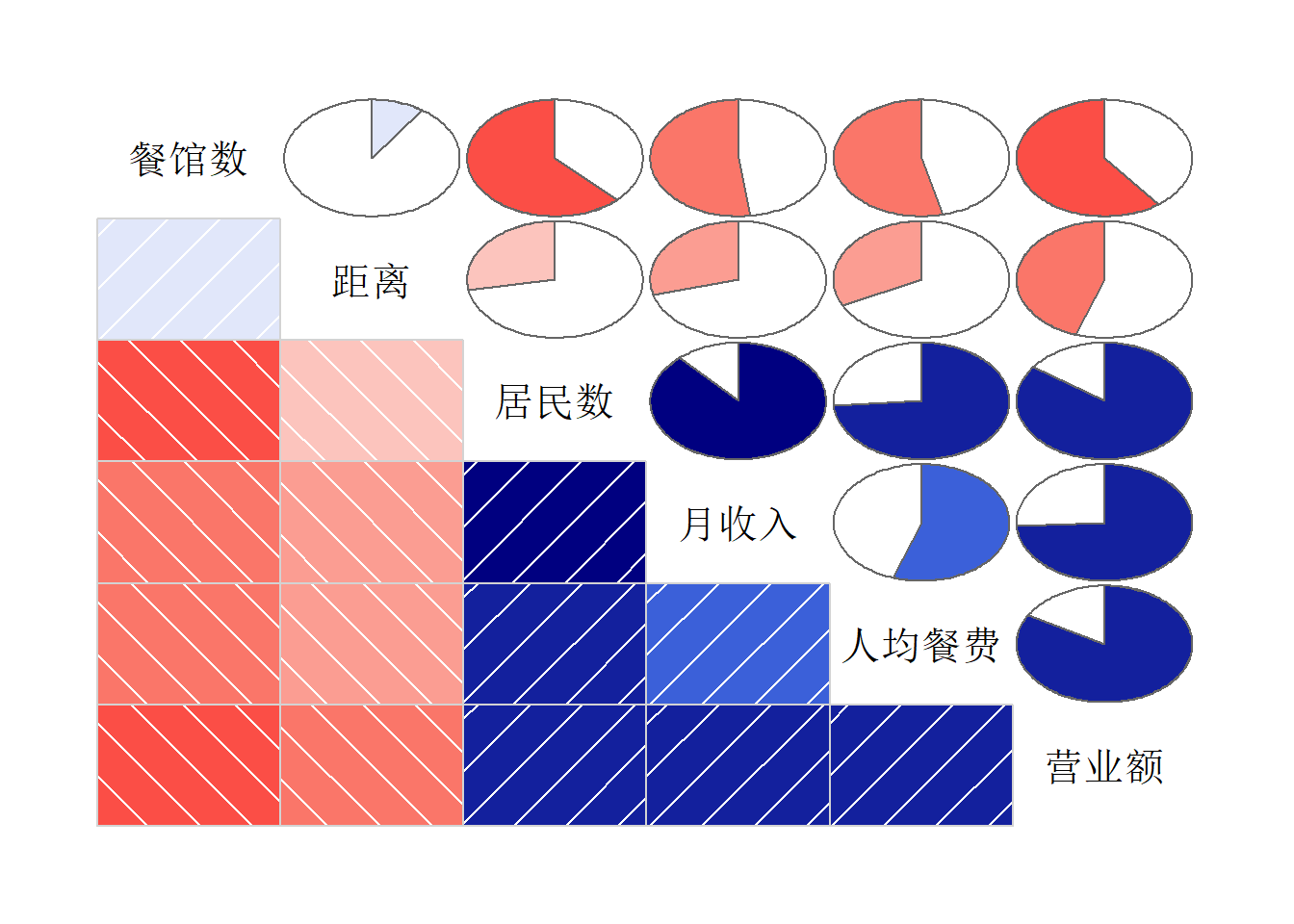
##
## Call:
## lm(formula = 营业额 ~ 居民数 + 人均餐费 + 月收入 + 餐馆数 + 距离,
## data = Resturant)
##
## Residuals:
## Min 1Q Median 3Q Max
## -16.7204 -6.0600 0.7152 3.2144 21.4805
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.2604768 10.4679833 0.407 0.68856
## 居民数 0.1273254 0.0959790 1.327 0.20037
## 人均餐费 0.1605660 0.0556834 2.884 0.00952 **
## 月收入 0.0007636 0.0013556 0.563 0.57982
## 餐馆数 -0.3331990 0.3986248 -0.836 0.41362
## 距离 -0.5746462 0.3087506 -1.861 0.07826 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.65 on 19 degrees of freedom
## Multiple R-squared: 0.8518, Adjusted R-squared: 0.8128
## F-statistic: 21.84 on 5 and 19 DF, p-value: 2.835e-07在0.15水平上只有人均餐费和到市中心距离是显著的。 进行逐步回归筛选:
## Start: AIC=123.39
## 营业额 ~ 居民数 + 人均餐费 + 月收入 + 餐馆数 + 距离
##
## Df Sum of Sq RSS AIC
## - 月收入 1 35.96 2189.0 121.81
## - 餐馆数 1 79.17 2232.2 122.30
## <none> 2153.0 123.39
## - 居民数 1 199.42 2352.4 123.61
## - 距离 1 392.54 2545.6 125.58
## - 人均餐费 1 942.22 3095.2 130.47
##
## Step: AIC=121.81
## 营业额 ~ 居民数 + 人均餐费 + 餐馆数 + 距离
##
## Df Sum of Sq RSS AIC
## - 餐馆数 1 78.22 2267.2 120.69
## <none> 2189.0 121.81
## - 距离 1 445.69 2634.7 124.44
## - 人均餐费 1 925.88 3114.9 128.63
## - 居民数 1 1133.27 3322.3 130.24
##
## Step: AIC=120.69
## 营业额 ~ 居民数 + 人均餐费 + 距离
##
## Df Sum of Sq RSS AIC
## <none> 2267.2 120.69
## - 距离 1 404.28 2671.5 122.79
## - 人均餐费 1 1050.90 3318.1 128.21
## - 居民数 1 1661.83 3929.0 132.43##
## Call:
## lm(formula = 营业额 ~ 居民数 + 人均餐费 + 距离, data = Resturant)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.027 -5.361 -1.560 2.304 23.001
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.68928 6.25242 -0.270 0.78966
## 居民数 0.19022 0.04848 3.923 0.00078 ***
## 人均餐费 0.15763 0.05052 3.120 0.00518 **
## 距离 -0.56979 0.29445 -1.935 0.06656 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.39 on 21 degrees of freedom
## Multiple R-squared: 0.8439, Adjusted R-squared: 0.8216
## F-statistic: 37.85 on 3 and 21 DF, p-value: 1.187e-08最后进保留了周边居民人数、人均餐费、到市中心距离三个自变量, 删去了周边居民月收入和周边餐馆数两个自变量。
32.3.6 哑变量与变截距项的模型
32.3.6.1 哑变量
回归分析的因变量是连续型的,服从正态分布。 回归分析的自变量是数值型的,可以连续取值也可以离散取值。 但是,如果自变量是类别变量, 用简单的1,2,3编码并不能正确地表现不同类别的作用。 可以将类别变量转换成一个或者多个取0、1值的变量, 称为哑变量(dummy variables)或虚拟变量。
32.3.6.1.1 二值哑变量与平行线模型
如果\(f\)是一个二值分类变量,将其中一个类编码为1, 另一个类编码为零。 例如,\(f=1\)表示处理组,\(f=0\)表示对照组。 这样编码后二值分类变量可以直接用在回归模型中。
例如 \[ Ey = \beta_0 + \beta_1 x + \beta_2 f \] 相当于 \[\begin{aligned} Ey = \begin{cases} \beta_0 + \beta_1 x, & \text{对照组} \\ (\beta_0 + \beta_2) + \beta_1 x, & \text{处理组} \end{cases} \end{aligned}\] 这样的模型叫做平行线模型, 处理组的数据与对照组的数据服从斜率相同、截距不同的一元线性回归模型。 比每个组单独建模更有效。
如果检验: \[H_0: \beta_2 = 0\] 则不显著时, 可以认为在处理组和对照组中\(y\)与\(x\)的关系没有显著差异。
进一步考虑 \[ Ey = \beta_0 + \beta_1 x + \beta_2 f + \beta_3 f x \] 相当于 \[\begin{aligned} Ey = \begin{cases} \beta_0 + \beta_1 x, & \text{对照组} \\ (\beta_0 + \beta_2) + (\beta_1 + \beta_3) x, & \text{处理组} \end{cases} \end{aligned}\] 比每个组单独建立回归模型更有效。 可以检验 \[H_0: \beta_3=0\] 不显著时可以用平行线模型。
比如,为了表示男生和女生的体重有不同, 可以在以体重为因变量的回归中加入自变量性别:
##
## Call:
## lm(formula = weight ~ height + sex, data = d.class)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.7627 -5.9583 -0.3682 8.7725 15.7758
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -126.1687 34.6352 -3.643 0.00219 **
## height 3.6789 0.5392 6.823 4.09e-06 ***
## sexF -6.6208 5.3887 -1.229 0.23697
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.06 on 16 degrees of freedom
## Multiple R-squared: 0.7903, Adjusted R-squared: 0.7641
## F-statistic: 30.15 on 2 and 16 DF, p-value: 3.74e-06结果中的sexM项表示以女生为基数,男生体重的平均增加量。 这一项不显著。
有些例子中如果忽略了分类变量, 结论可能是错误的。 例如, 考察iris数据中花萼长宽之间的关系。 数据中有三个品种的花, 仅考虑其中的setosa和versicolor两个品种。
d <- iris[iris[["Species"]] %in% c("setosa", "versicolor"),
c("Sepal.Length", "Sepal.Width", "Species")]
d$Species <- factor(as.character(d$Species))
lm7 <- lm(Sepal.Width ~ Sepal.Length, data=d)
with(d, plot(Sepal.Length, Sepal.Width, col=(2:3)[Species]))
with(d, legend("topleft", pch=1, col=2:3, legend=levels(Species)))
abline(lm7, lwd=2)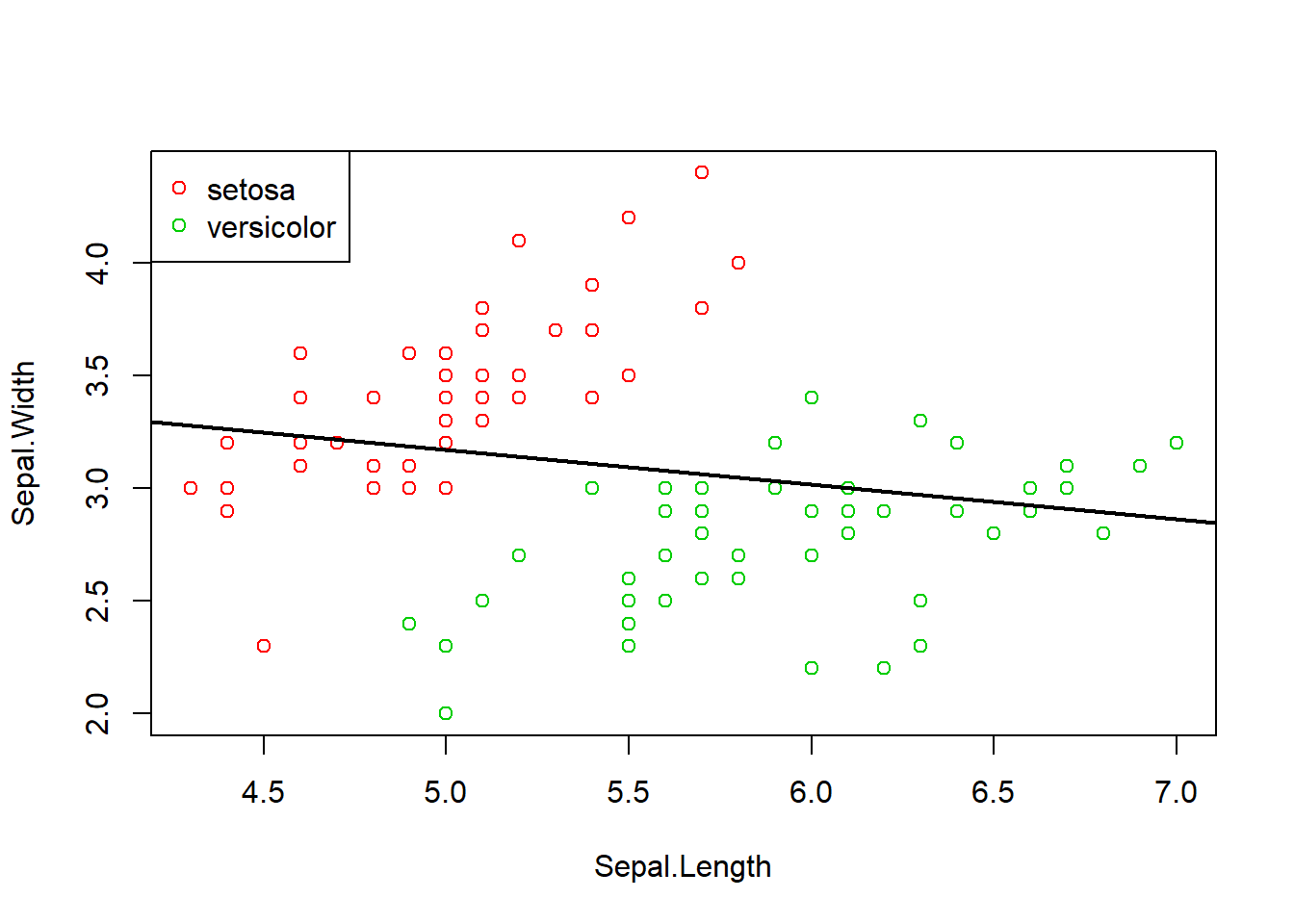
##
## Call:
## lm(formula = Sepal.Width ~ Sepal.Length, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.17136 -0.26382 -0.04468 0.29966 1.33618
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.93951 0.40621 9.698 5.47e-16 ***
## Sepal.Length -0.15363 0.07375 -2.083 0.0398 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4709 on 98 degrees of freedom
## Multiple R-squared: 0.04241, Adjusted R-squared: 0.03263
## F-statistic: 4.34 on 1 and 98 DF, p-value: 0.03984回归结果花萼长、宽是负相关的, 这明显不合理,出现了“悖论”。 实际是因为两个品种的样本混杂在一起了。
加入Species分类变量作为回归自变量:
##
## Call:
## lm(formula = Sepal.Width ~ Species + Sepal.Length, data = d)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.88917 -0.14677 -0.02517 0.16643 0.64444
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.06519 0.32272 3.301 0.00135 **
## Speciesversicolor -1.09696 0.08170 -13.427 < 2e-16 ***
## Sepal.Length 0.47200 0.06398 7.377 5.51e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2799 on 97 degrees of freedom
## Multiple R-squared: 0.665, Adjusted R-squared: 0.6581
## F-statistic: 96.28 on 2 and 97 DF, p-value: < 2.2e-16现在花萼长度变量的系数为正而且高度显著。
两个品种区别的变量Speciesversicolor表示versicolor品种取1,
setosa取0的哑变量。
versicolor品种的花萼宽度与setosa相比在长度相等的情况下平均较小。
作两条回归直线的图形:
with(d, plot(Sepal.Length, Sepal.Width, col=(2:3)[Species]))
with(d, legend("topleft", pch=1, col=2:3, legend=levels(Species)[1:2]))
abline(a=coef(lm8)[1], b=coef(lm8)[3], col=2, lwd=2)
abline(a=sum(coef(lm8)[1:2]), b=coef(lm8)[3], col=3, lwd=2)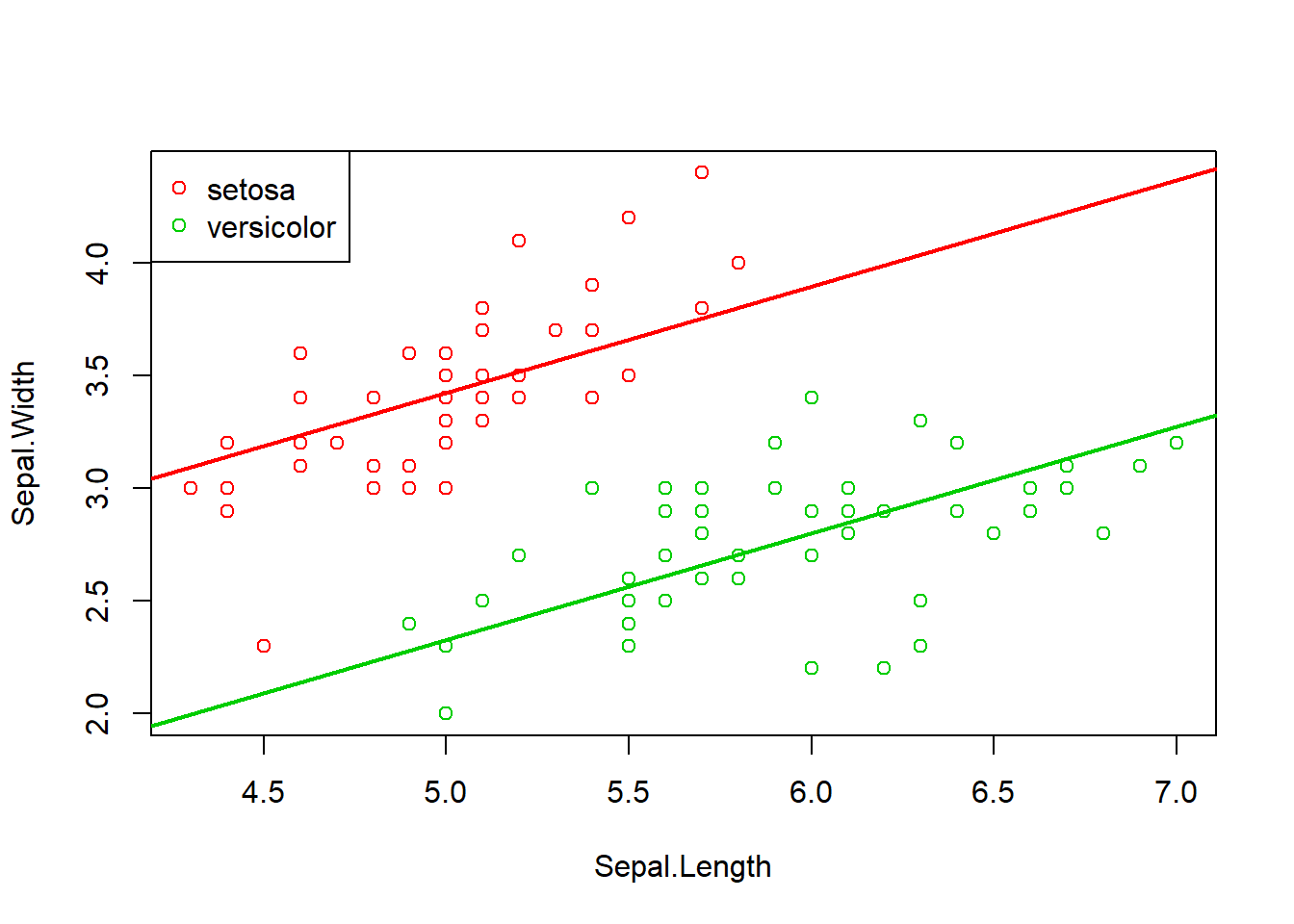
32.3.6.1.2 多值哑变量
如果变量\(f\)是一个有\(k\)分类的变量, 可以将\(f\)变成\(k-1\)个取0、1值的哑变量 \(z_1, z_2, \dots, z_{k-1}\)。
例如,\(f\)取三种不同的类别,可以转换为两个哑变量\(z_1, z_2\), 常用的编码方式为: \[\begin{aligned} & f=1 \Leftrightarrow (z_1, z_2)=(0,0), \\ & f=2 \Leftrightarrow (z_1, z_2)=(1,0), \\ & f=3 \Leftrightarrow (z_1, z_2)=(0,1) \end{aligned}\] 这是将\(f=1\)看成对照组。
在R中,
用model.matrix(y ~ x1 + f, data=d)
可以生成将因子f转换成哑变量后的包含因变量和自变量的矩阵。
32.3.7 残差诊断
先复习一些回归理论。 将模型写成矩阵形式 \[ {\boldsymbol Y} = {\boldsymbol X}\boldsymbol\beta + \boldsymbol\varepsilon \] \({\boldsymbol Y}\)为\(n \times 1\)向量, \({\boldsymbol X}\)为\(n \times p\)矩阵, 一般第一列元素全是1, 代表截距项。 \(\boldsymbol\beta\)为\(p \times 1\)未知参数向量; \(\boldsymbol\varepsilon\)为\(n \times 1\)随机误差向量, \(\varepsilon\)的元素独立且方差为相等的\(\sigma^2\)(未知)。
假设矩阵\(\boldsymbol X\)满秩,系数的估计为 \[\begin{aligned} \hat{\boldsymbol\beta} = \left( {{\boldsymbol X^T \boldsymbol X}} \right)^{-1} {\boldsymbol X^T \boldsymbol Y} \end{aligned}\]
拟合值(或称预报值)向量为 \[\begin{aligned} \hat{\boldsymbol Y} = {\boldsymbol X} \left( {{\boldsymbol X \boldsymbol X}} \right)^{-1} {\boldsymbol X^T \boldsymbol Y} = {\boldsymbol H \boldsymbol Y} \end{aligned}\] 其中\({\boldsymbol H} = {\boldsymbol X}\left( {{\boldsymbol X'X}} \right)^{-1} {\boldsymbol X'}\) 是\(R^n\)空间的向量向\({\boldsymbol X}\) 的列张成的线性空间\(\mu({\boldsymbol X})\) 投影的投影算子矩阵, 叫做帽子矩阵。 设\(\boldsymbol H = \left( h_{ij} \right)_{n\times n}\)。
拟合残差向量为 \[\begin{aligned} \boldsymbol e = {\boldsymbol Y} - \hat{\boldsymbol Y} = ({\boldsymbol I} - {\boldsymbol H}){\boldsymbol Y} \end{aligned}\] 残差平方和为 \[\begin{aligned} \mbox{ESS} = \boldsymbol e^T \boldsymbol e = \sum\limits_{i = 1}^n {\left( {Y_i - \hat Y_i } \right)^2 } \end{aligned}\]
误差项方差的估计 (要求设计阵\({\boldsymbol X}\)满秩)为均方误差(MSE) \[\begin{aligned} \hat\sigma^2 = \mbox{MSE} = \frac{1}{{n - p}} \mbox{ESS} \end{aligned}\] (其中\(p\)在有截距项时是自变量个数加1)
在线性模型的假设下, 若设计阵\({\boldsymbol X}\)满秩, \(\hat\beta\)和\(\hat\sigma^2\) 分别是\(\beta\)和\(\sigma^2\)的无偏估计。
系数估计的方差阵 \[ \text{Var}(\hat{\boldsymbol\beta}) = \sigma^2 \left( {\boldsymbol X}' {\boldsymbol X} \right)^{-1} \]
回归残差及其方差为 \[\begin{aligned} e_i =& y_i - \hat y_i, \quad i=1,2,\dots,n \\ \text{Var}(e_i) =& \sigma^2 (1 - h_{ii}) \quad(h_{ii}\text{是}H\text{的主对角线元素}) \end{aligned}\]
若lmres是R中lm()的回归结果,
用residuals(lmres)可以求残差。
把\(e_i\)除以其标准差估计, 称为标准化残差,或内部学生化残差: \[\begin{aligned} r_i = \frac{e_i}{s \sqrt{1 - h_{ii}}}, \quad i=1,2,\dots,n \end{aligned}\] \(r_i\)渐近服从正态分布。
若lmres是R中lm()的回归结果,
用rstandard(lmres)可以求标准化残差。
如果计算\(y_i\)的预测值时, 删除第\(i\)个观测后建立回归模型得到\(\sigma^2\) 的估计\(s_{(i)}^2\), 则外部学生化残差为 \[\begin{aligned} t_i = \frac{e_i}{s_{(i)} \sqrt{1 - h_{ii}}} \end{aligned}\] \(t_i\)近似服从\(t(n-p-1)\)分布 (有截距项时\(p\)等于自变量个数加1)。 其中\(s_{(i)}\)有简单公式: \[\begin{aligned} s_{(i)}^2 = \frac{n-p-r_i^2}{n-p-1} \hat\sigma^2 \end{aligned}\]
若lmres是R中lm()的回归结果,
用rstudent(lmres)可以求外部学生化残差。
在R中,
与一元回归的诊断类似。
用plot()作4个残差诊断图。
可以用which=1指定仅作第一幅图。
如餐馆营业额例子的残差诊断:
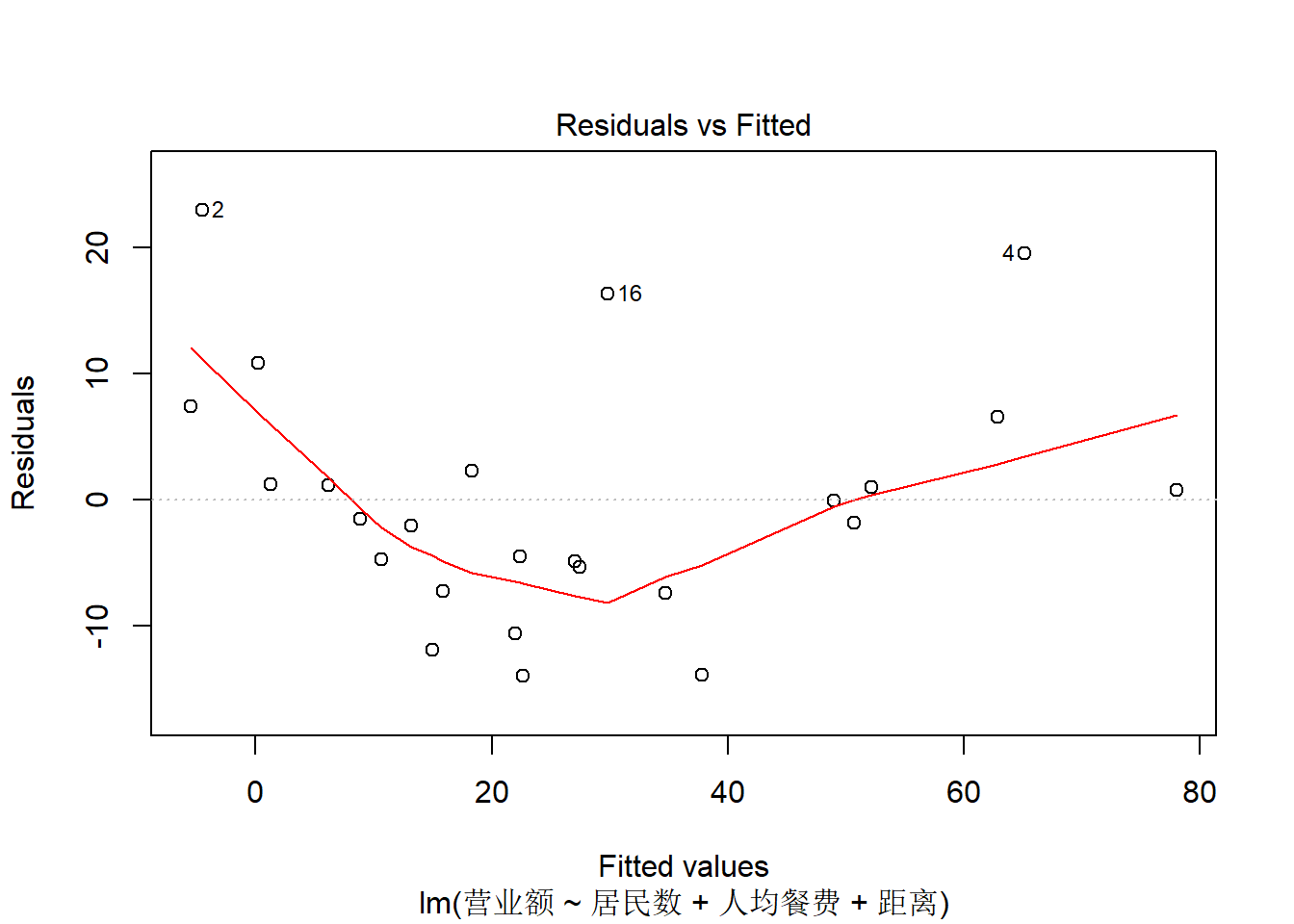
上图是残差对拟合值的散点图, 可以查看有无非线性。 有轻微的非线性关系。
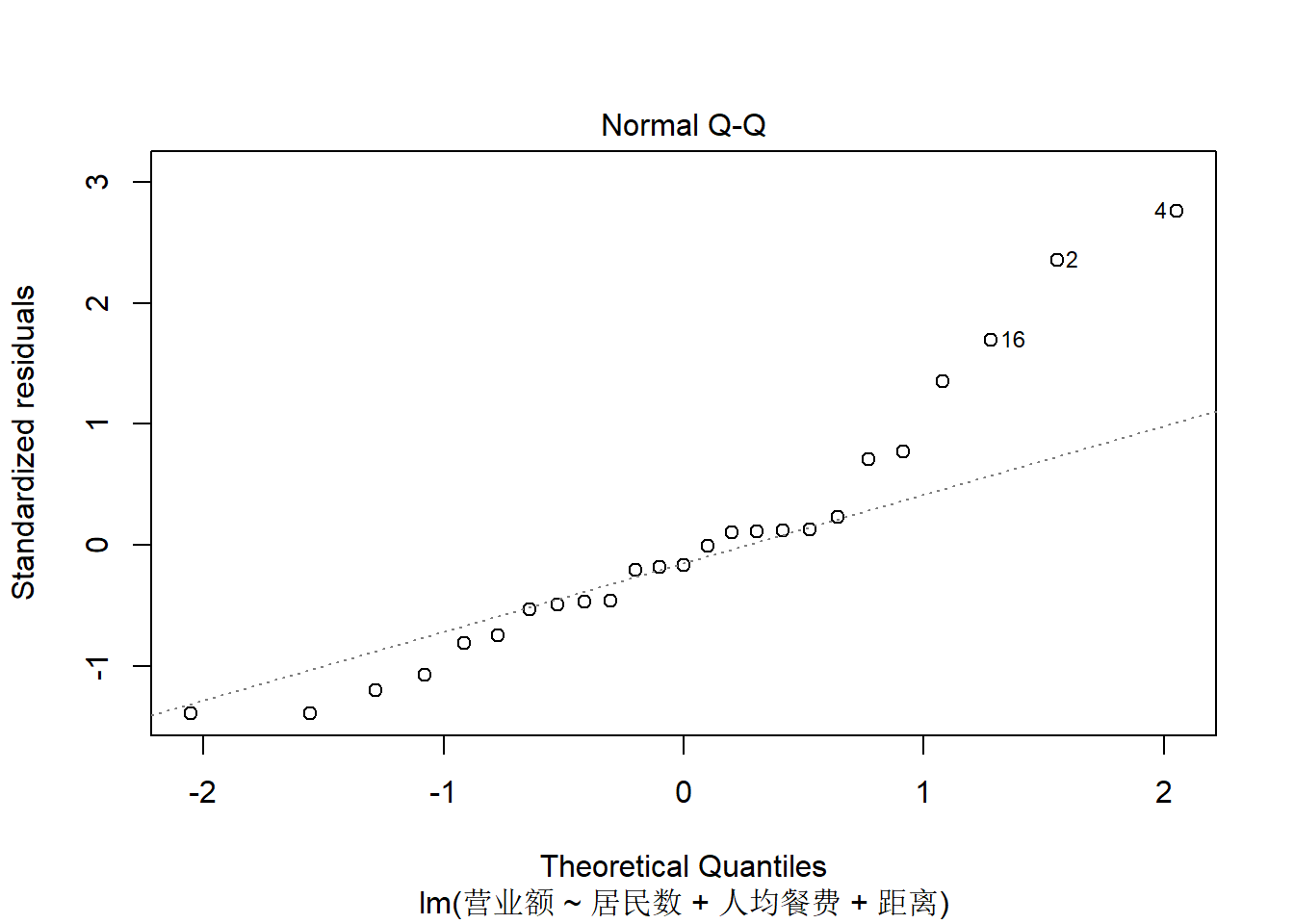
上图是残差的正态QQ图, 查看残差是否正态分布。 残差分布略有右偏,不算太严重。
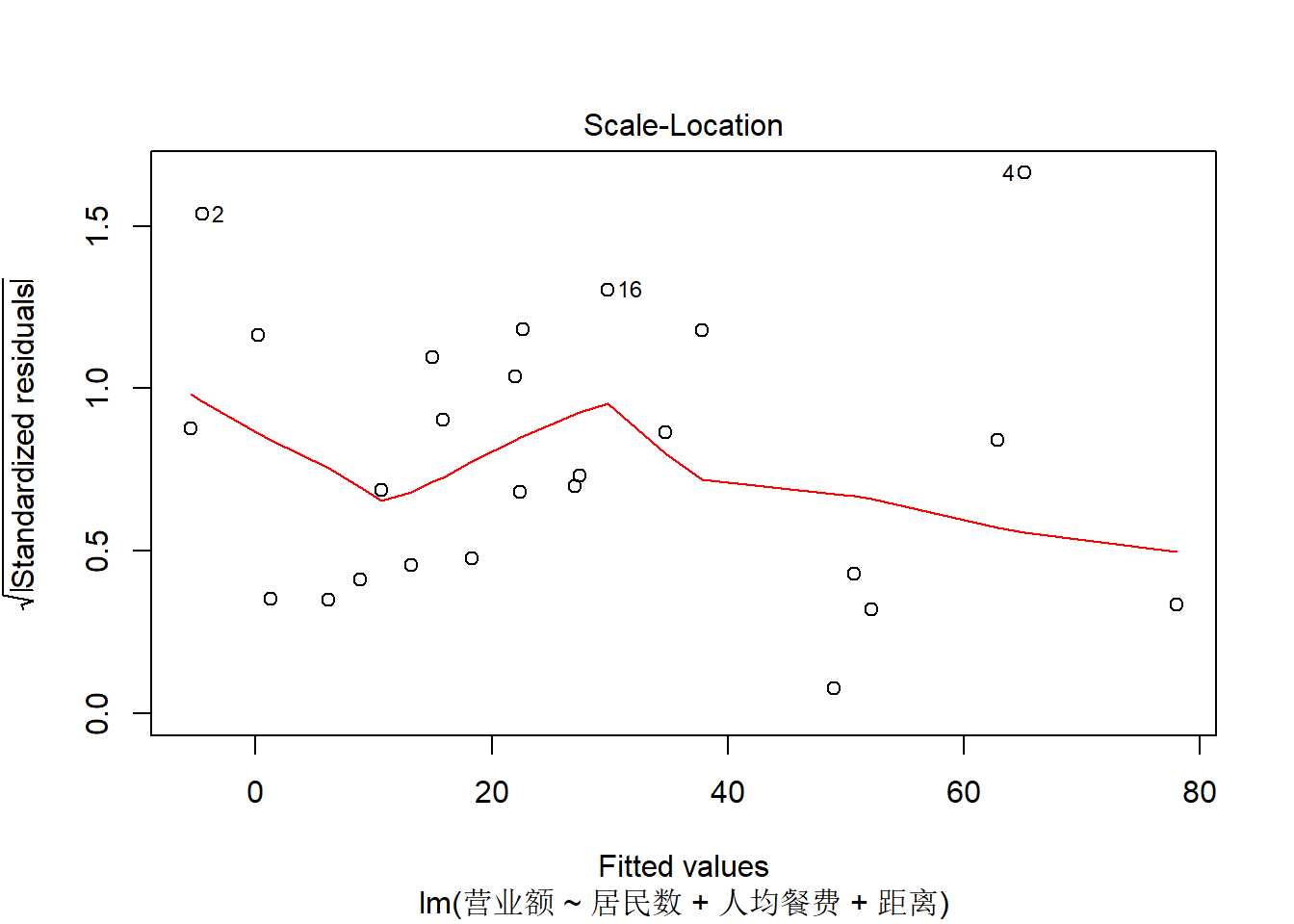 上图是标准化残差绝对值平方根对拟合值的散点图,
可以查看是否有异方差。
没有明显的异方差。
上图是标准化残差绝对值平方根对拟合值的散点图,
可以查看是否有异方差。
没有明显的异方差。

上图用来查看强影响点, 4号观测是一个强影响点。
货运公司例子的多元回归的残差诊断:
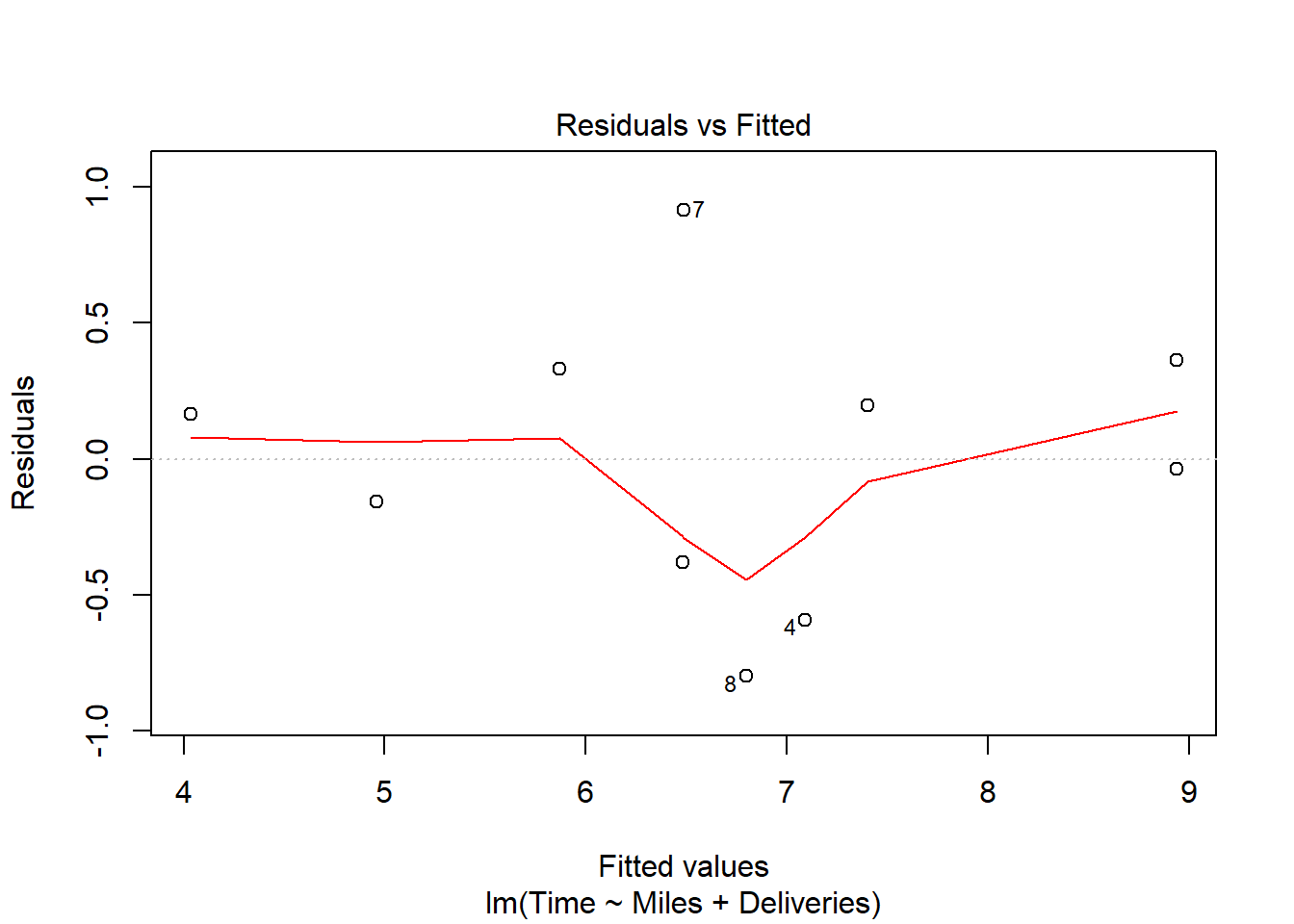
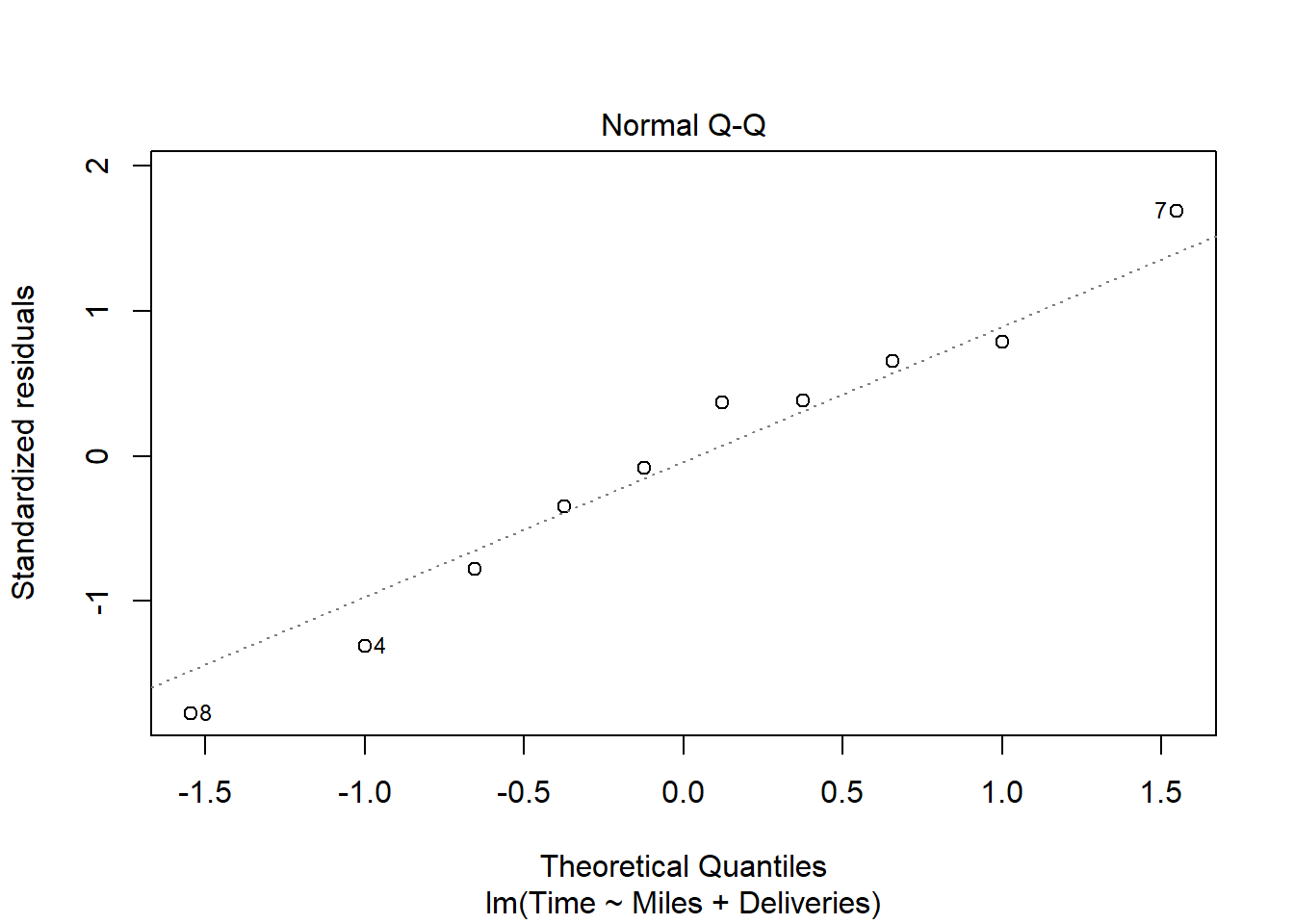
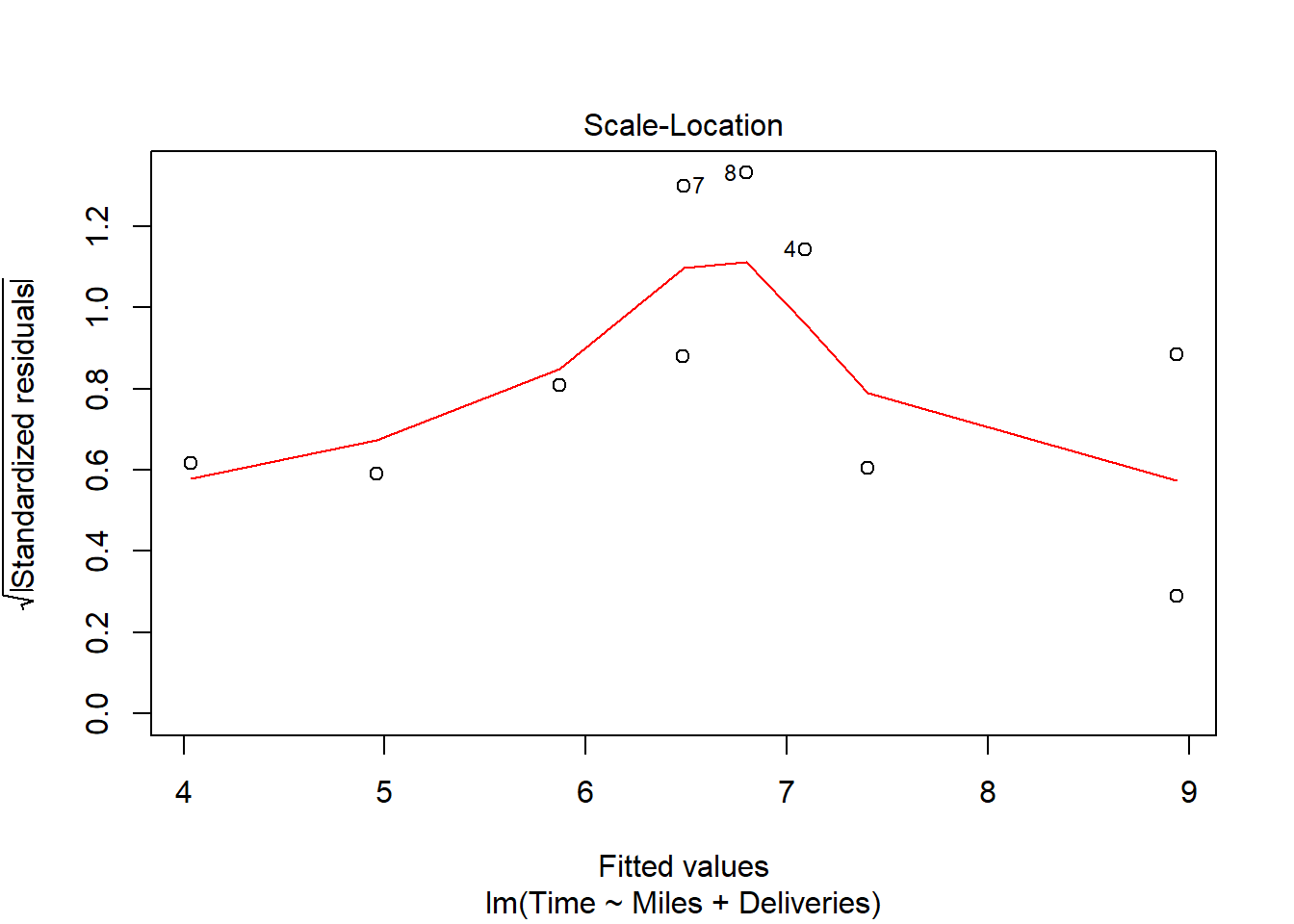
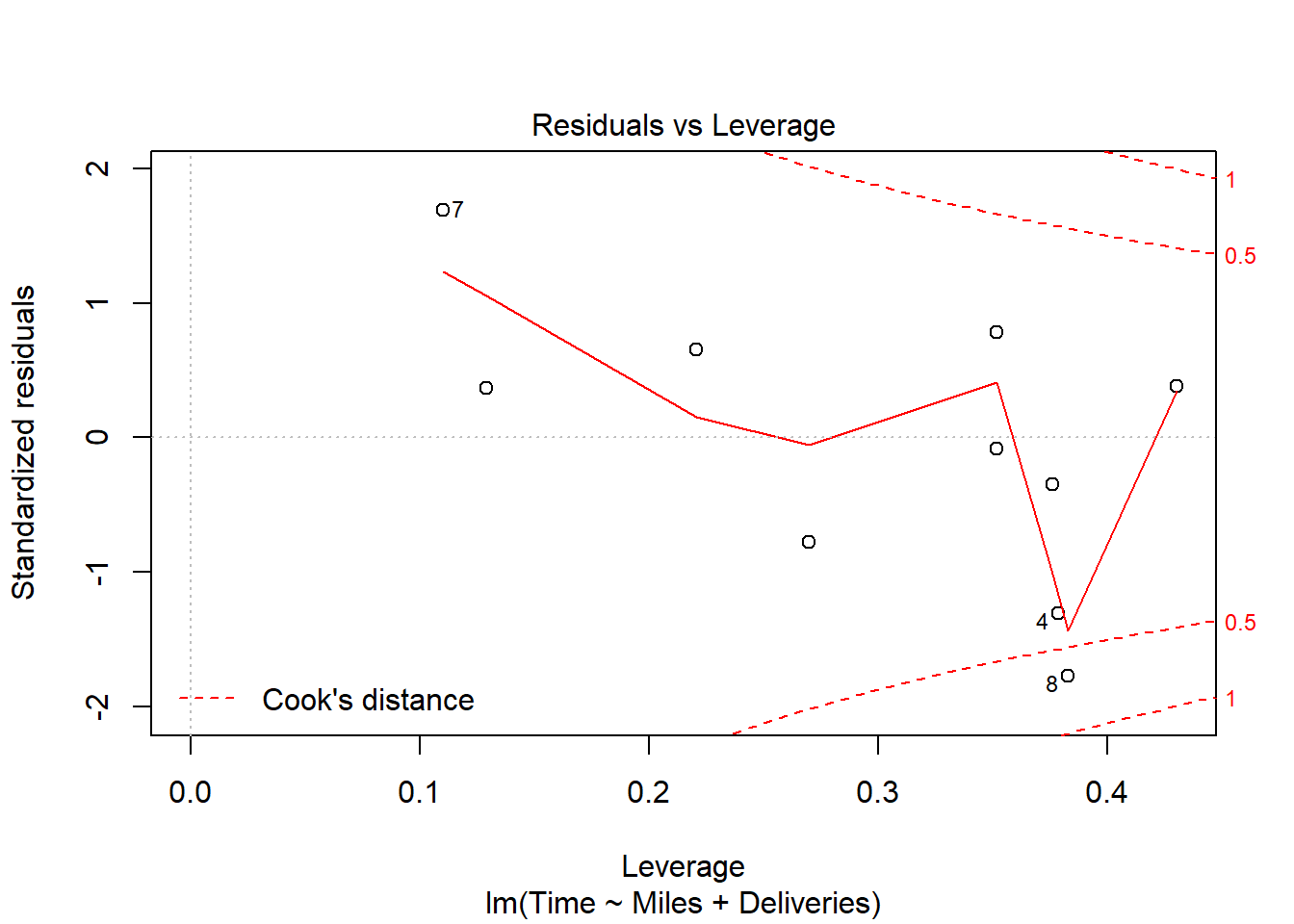
有一定的异方差倾向,但是数据量不大就不做处理。
32.3.8 多重共线性
狭义的多重共线性(multicollinearity): 自变量的数据存在线性组合近似地等于零, 使得矩阵求解回归系数时结果不稳定, 回归结果很差。
广义的多重共线性: 自变量之间存在较强的相关性, 这样自变量是联动的, 互相之间有替代作用。 甚至于斜率项的正负号都因为这种替代作用而可能是错误的方向。
例如, 餐馆营业额例子中, F检验显著, 5个自变量如果用在一元回归中斜率项都显著, 但是在多元回归中, 在0.15水平下仅有人均餐费和到市中心的距离的系数是显著的, 月收入、餐馆数、居民数的系数不显著。
但是实际上,单独使用这三个自变量作一元线性回归, 结果都是显著的:
##
## Call:
## lm(formula = 营业额 ~ 月收入, data = Resturant)
##
## Residuals:
## Min 1Q Median 3Q Max
## -32.151 -10.725 -0.696 6.033 47.819
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.484580 5.955478 0.081 0.936
## 月收入 0.004995 0.000944 5.291 2.27e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 16.88 on 23 degrees of freedom
## Multiple R-squared: 0.549, Adjusted R-squared: 0.5294
## F-statistic: 27.99 on 1 and 23 DF, p-value: 2.273e-05如何识别多重共线性?
如果两个自变量之间的相关系数显著地不等于零, 这两个自变量就有广义的共线性。
如果线性关系的F检验显著但是单个回归系数都不显著, 可能是由于多重共线性。
如果有单个回归系数显著但是\(F\)检验不显著, 可能是由于多重共线性。
如果某些回归系数的正负号与通常的认识相反, 可能是由于多重共线性。
将第\(i\)个自变量\(x_i\)作为因变量, 用其它的\(p-1\)个自变量作为自变量作多元线性回归, 得到一个复相关系数平方\(R_i^2\), 这个\(R_i^2\)接近于1时\(x_i\)与其他自变量之间存在多重共线性。 令\(x_i\)的容忍度(tolerance)等于\(1-R_i^2\), 容忍度接近于0时存在多重共线性。
容忍度小于0.1时多重共线性为严重程度。
称容忍度的倒数为方差膨胀因子(VIF), VIF大于10或者大于5作为严重的多重共线性。
为了计算VIF, 首先把矩阵\(X^T X\)看成一个协方差阵, 把它转换为相关系数阵设为\(M\), 则\(M^{-1}\)的各主对角线元素就是各个VIF。
car包的vif()函数计算方差膨胀因子。
如:
## 居民数 人均餐费 月收入 餐馆数 距离
## 8.233159 2.629940 5.184365 1.702361 1.174053可以认为变量“居民数”和“月收入”有共线问题。
做共线诊断还可以用条件数(Conditional Index): 这是一个正数,用来衡量\((X^T X)^{-1}\)的稳定性, 定义为\(X^T X\)的最大特征值与最小特征值之比。 条件数在0—100之间时认为无共线性, 在100—1000之间时认为自变量之间有中等或较强共线性, 在1000以上认为自变量之间有强共线性。
解决多重共线性问题, 最简单的方法是回归自变量选择, 剔除掉有严重共线性的自变量, 这些自变量的信息可以由其他变量代替。 还可以对自变量作变换,如用主成分分析降维。 可以用收缩方法如岭回归、lasso回归等。
32.3.9 强影响点分析
强影响点是删去以后严重改变参数估计值的观测。 包括自变量取值离群和因变量拟合离群的点。
杠杆(leverage)指帽子矩阵的对角线元素\(h_{ii}\), \[\begin{aligned} \frac{1}{n} \leq h_{ii} \leq \frac{1}{d_i} \end{aligned}\] 其中\(d_i\)是第\(i\)个观测的重复观测次数。 某观测杠杆值高说明该观测自变量有异常值。 杠杆值大于\(2p/n\)的观测需要仔细考察 (有截距项时\(p\)等于自变量个数加1)。
若lmres是R中lm()的回归结果,
用hatvalues(lmres)可以求杠杆值。
考察外学生化残差\(t_i\), 绝对值超过2的观测拟合误差大, 在\(y\)方向离群,需要关注。
若lmres是R中lm()的回归结果,
用rstudent(lmres)可以求外学生化。
Cook距离统计量: \[\begin{aligned} D_i = \frac{1}{p} r_i^2 \frac{h_{ii}}{1 - h_{ii}} \end{aligned}\] 包含了\(y\)方向的离群\(r_i\)和\(x\)方向的离群\(h_{ii}\)的信息。 超过\(\frac{4}{n}\)的值需要注意。
若lmres是R中lm()的回归结果,
用cooks.distance(lmres)可以求Cook距离。
R中的强影响点诊断函数还有
dfbetas(), dffits(),
covratio()。
偏杠杆值衡量每个自变量(包括截距项)对杠杆的贡献。 把第j个自变量关于其它自变量回归得到残差, 第i个残差的平方占总残差平方和的比例为第j自变量在第i观测处的偏杠杆值。 偏杠杆值影响自变量选择时对该变量的选择。
32.3.10 过度拟合示例
\(R^2\)代表了模型对数据的拟合程度, 模型中加入的自变量越多, \(R^2\)越大。 是不是模型中的自变量越多越好? 可能会发生“过度拟合”。 用来建模的数据都拟合误差很小, 但是模型很难有合理解释, 对新的数据的预测效果很差甚至于完全错误。
set.seed(10)
n <- 20
x <- sample(1:n, size=n, replace=TRUE)
a <- 100
b <- 2
sigma <- 5
y <- a + b*x + rt(n, 4)*sigma
xnew <- c(1.5, 2.5, 3.5)
ynew <- a + b*xnew + rnorm(length(xnew), 0, sigma)
plot(x, y, pch=16, xlim=c(0, n+1), ylim=c(90,140))
points(xnew, ynew, pch=2, col="red")
legend("topleft", pch=c(16,2), col=c("black", "red"),
legend=c("拟合用", "测试用"))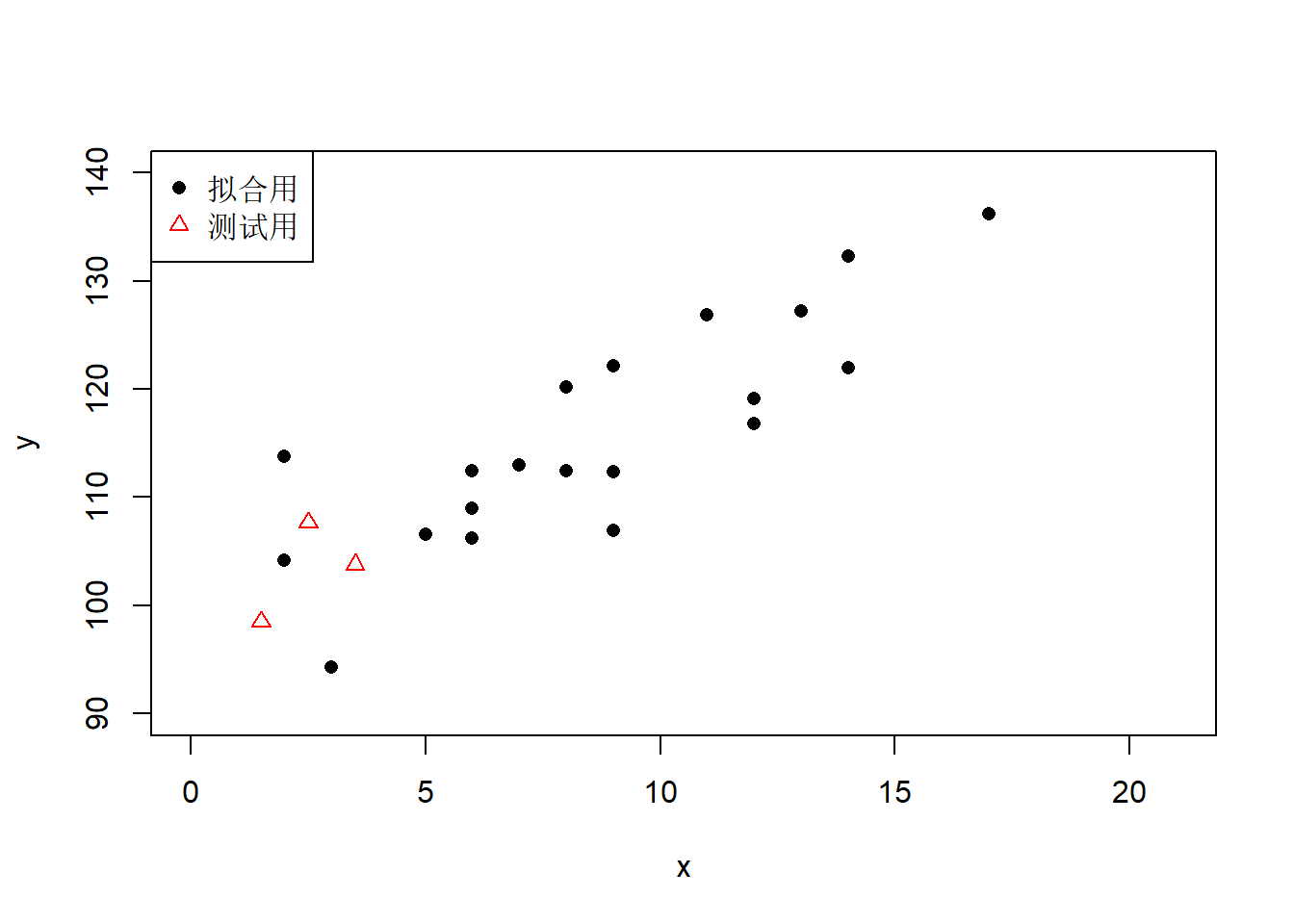
作线性回归:
plot(x, y, pch=16, xlim=c(0, n+1), ylim=c(90,140))
points(xnew, ynew, pch=2, col="red")
lmof1 <- lm(y ~ x)
abline(lmof1)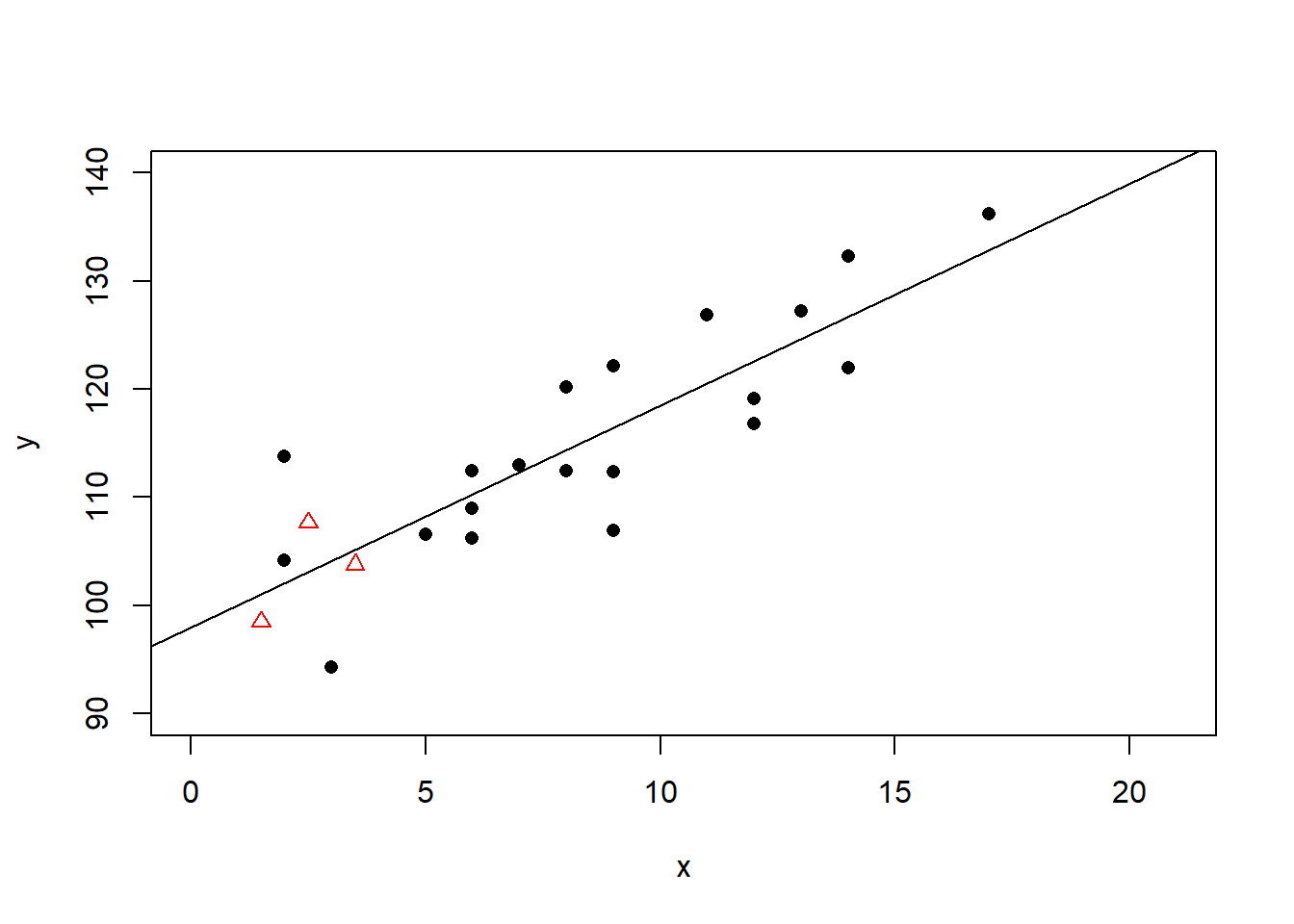
回归系数:
##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.8206 -4.0691 -0.2855 3.9371 11.7011
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 97.9570 3.0244 32.388 < 2e-16 ***
## x 2.0521 0.3163 6.489 4.21e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.767 on 18 degrees of freedom
## Multiple R-squared: 0.7005, Adjusted R-squared: 0.6839
## F-statistic: 42.1 on 1 and 18 DF, p-value: 4.209e-06二次多项式回归:
plot(x, y, pch=16, xlim=c(0, n+1), ylim=c(90,140))
points(xnew, ynew, pch=2, col="red")
lmof2 <- lm(y ~ x + I(x^2))
xx <- seq(1, n, length=100)
yy <- predict(lmof2, newdata=data.frame(x=xx))
lines(xx, yy)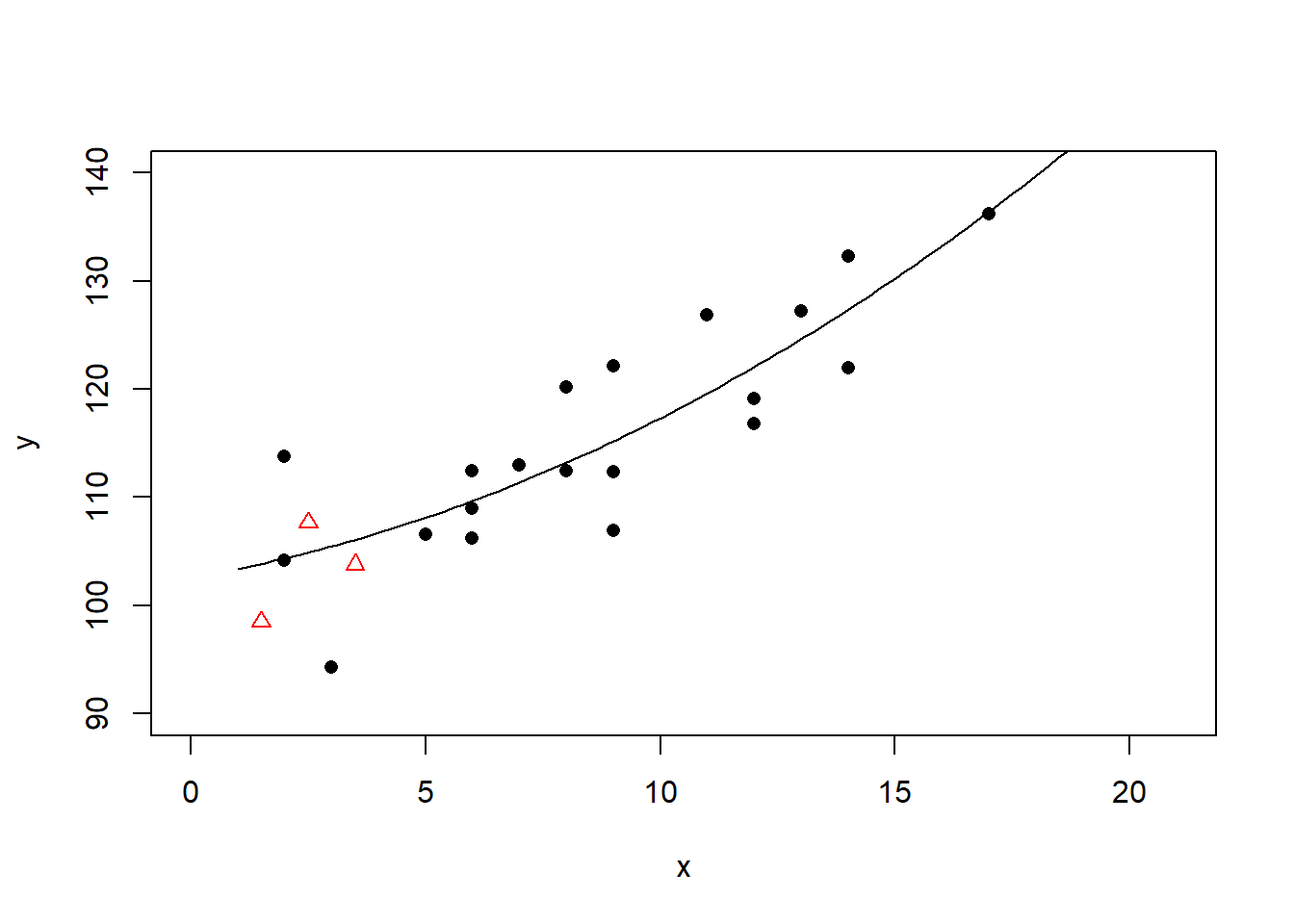
回归系数:
##
## Call:
## lm(formula = y ~ x + I(x^2))
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.175 -3.059 -0.439 3.358 9.400
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 102.59339 5.32854 19.254 5.57e-13 ***
## x 0.73688 1.28561 0.573 0.574
## I(x^2) 0.07371 0.06985 1.055 0.306
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.749 on 17 degrees of freedom
## Multiple R-squared: 0.7189, Adjusted R-squared: 0.6859
## F-statistic: 21.74 on 2 and 17 DF, p-value: 2.066e-05这个回归结果出现了多重共线性问题。 也已经过度拟合。
三次多项式回归:
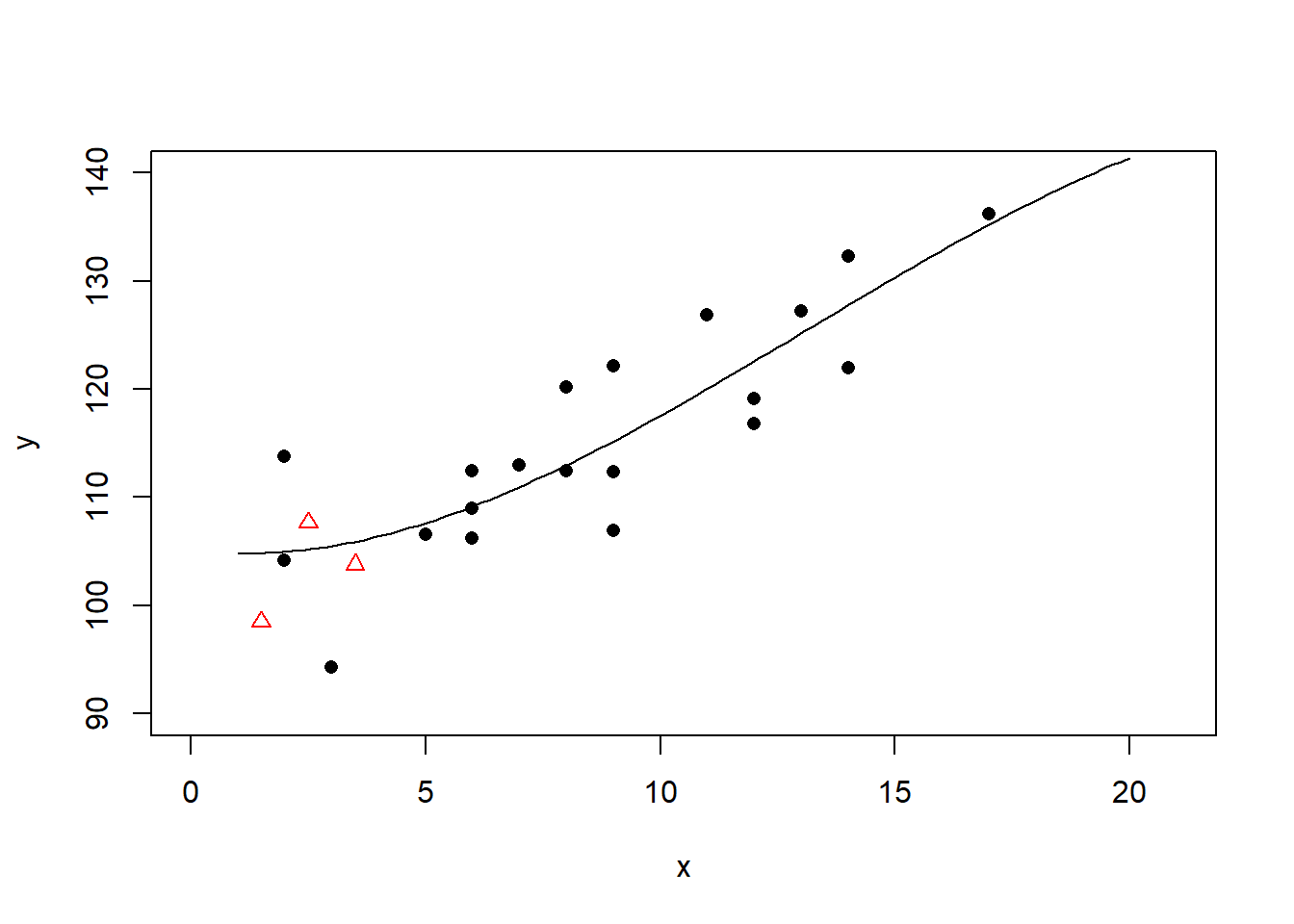
回归系数:
##
## Call:
## lm(formula = y ~ x + I(x^2) + I(x^3))
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.1976 -3.0835 -0.3567 3.6324 8.8020
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 105.162401 8.827478 11.913 2.29e-09 ***
## x -0.558534 3.734856 -0.150 0.883
## I(x^2) 0.240987 0.456853 0.527 0.605
## I(x^3) -0.006124 0.016518 -0.371 0.716
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.901 on 16 degrees of freedom
## Multiple R-squared: 0.7213, Adjusted R-squared: 0.6691
## F-statistic: 13.8 on 3 and 16 DF, p-value: 0.0001053这个回归结果出现了多重共线性问题。 也已经过度拟合。
四次多项式回归:
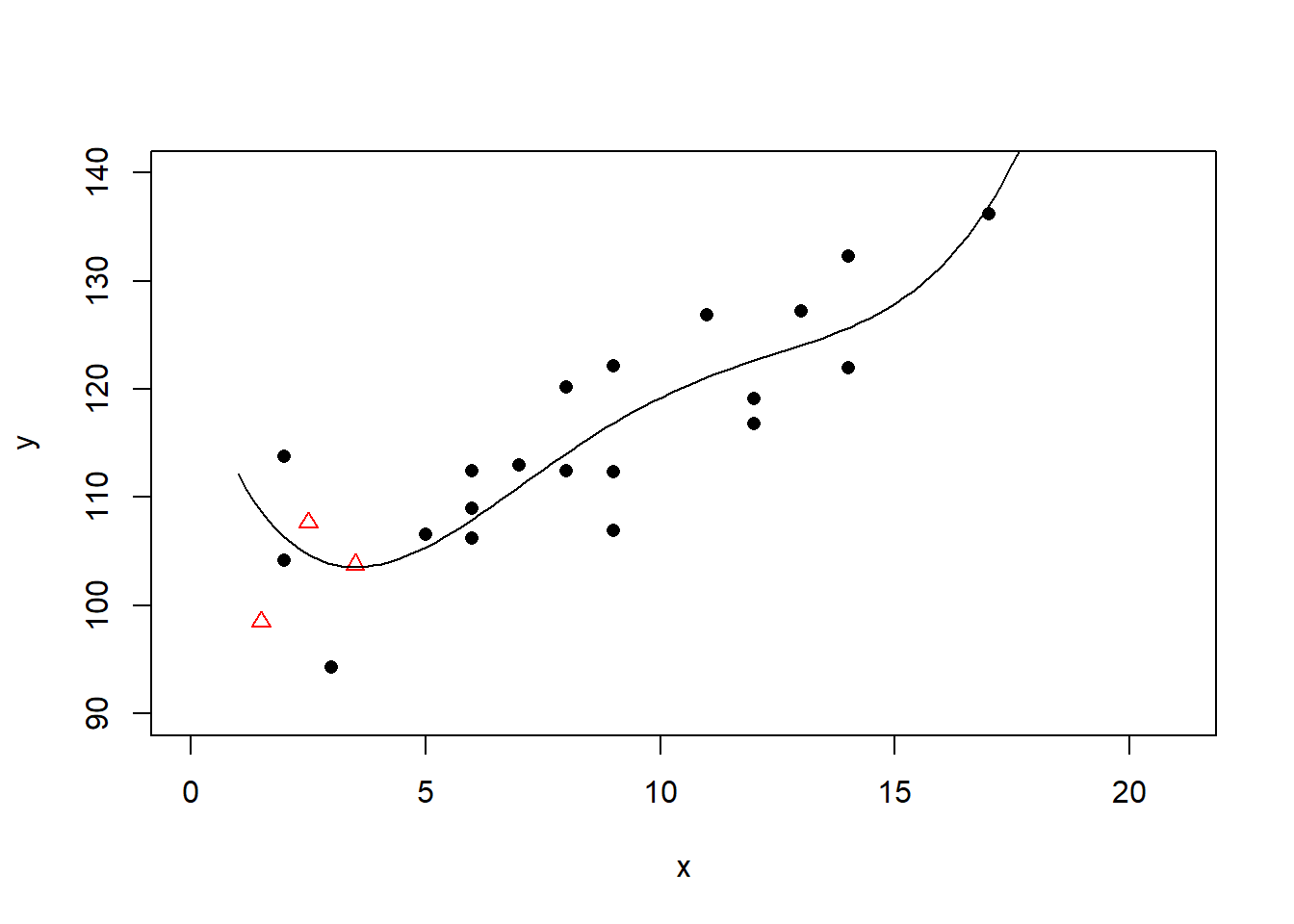
回归系数:
##
## Call:
## lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4))
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.8975 -3.5647 0.1241 4.7063 7.4675
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 122.380891 18.117315 6.755 6.47e-06 ***
## x -12.830942 11.890980 -1.079 0.298
## I(x^2) 2.785077 2.385359 1.168 0.261
## I(x^3) -0.206102 0.184800 -1.115 0.282
## I(x^4) 0.005273 0.004854 1.086 0.294
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.868 on 15 degrees of freedom
## Multiple R-squared: 0.7416, Adjusted R-squared: 0.6727
## F-statistic: 10.76 on 4 and 15 DF, p-value: 0.0002563五次多项式回归:
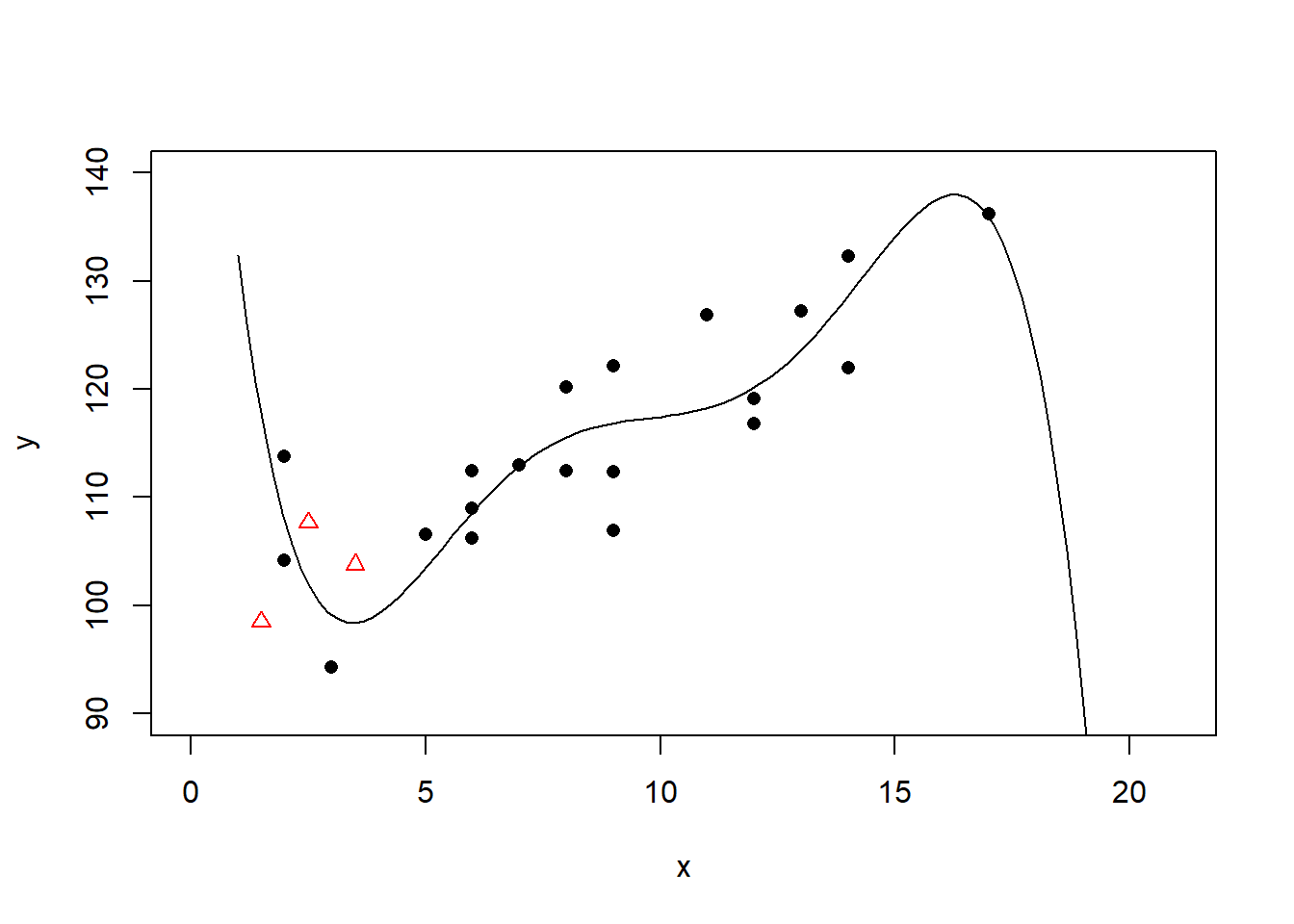
已经明显过度拟合。
回归系数:
##
## Call:
## lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4) + I(x^5))
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.9204 -3.4541 0.2201 3.7495 8.5922
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 181.846244 41.023546 4.433 0.000568 ***
## x -65.530939 34.875410 -1.879 0.081224 .
## I(x^2) 18.157919 9.886841 1.837 0.087594 .
## I(x^3) -2.170388 1.242055 -1.747 0.102453
## I(x^4) 0.118729 0.071167 1.668 0.117456
## I(x^5) -0.002418 0.001513 -1.598 0.132453
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.586 on 14 degrees of freedom
## Multiple R-squared: 0.7815, Adjusted R-squared: 0.7034
## F-statistic: 10.01 on 5 and 14 DF, p-value: 0.0003082六次多项式回归:
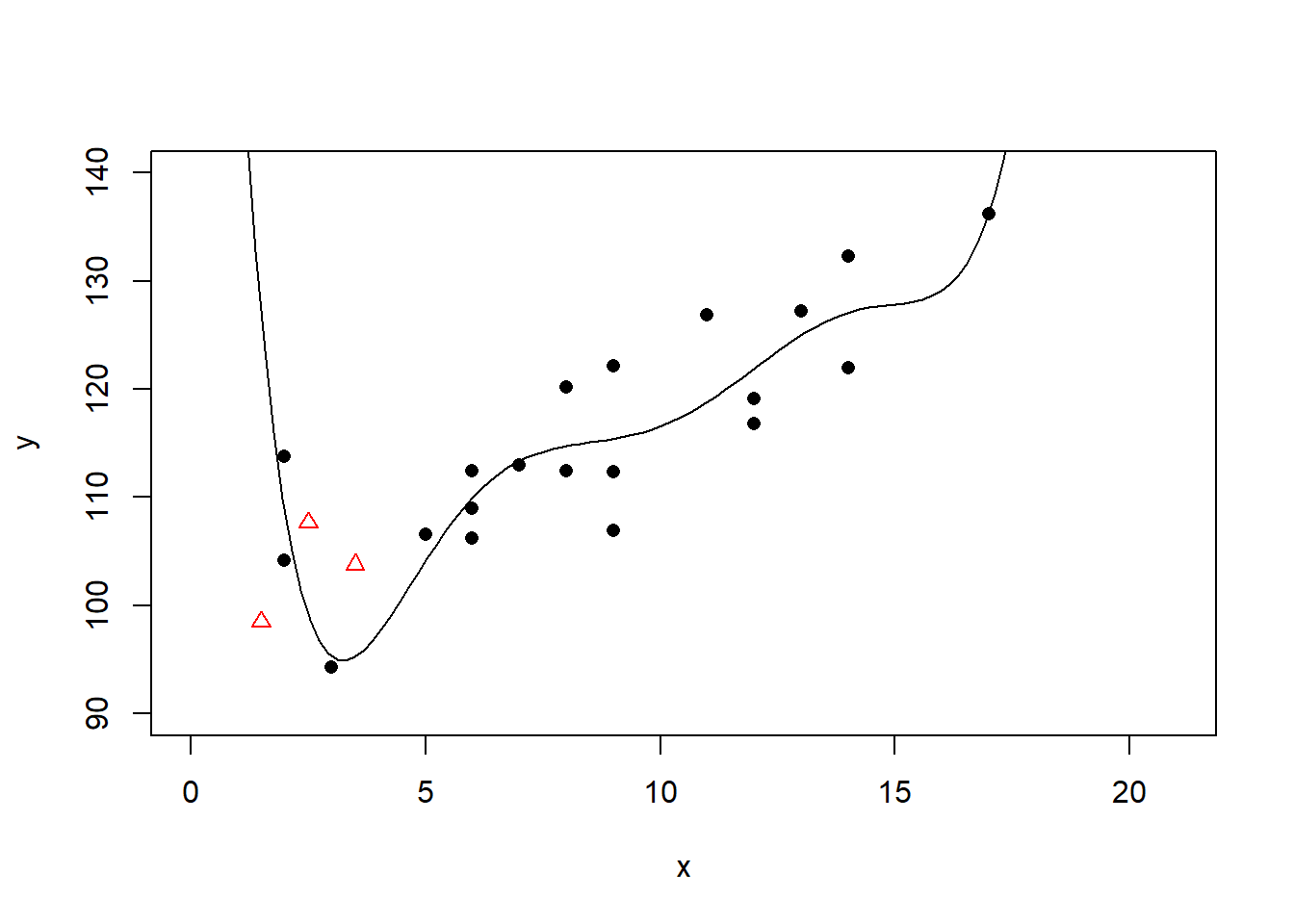
回归系数:
##
## Call:
## lm(formula = y ~ x + I(x^2) + I(x^3) + I(x^4) + I(x^5) + I(x^6))
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.4627 -3.2409 -0.6654 3.1208 8.0410
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.699e+02 8.387e+01 3.218 0.00673 **
## x -1.585e+02 8.483e+01 -1.868 0.08447 .
## I(x^2) 5.346e+01 3.103e+01 1.723 0.10864
## I(x^3) -8.572e+00 5.481e+00 -1.564 0.14188
## I(x^4) 7.158e-01 5.033e-01 1.422 0.17849
## I(x^5) -2.999e-02 2.307e-02 -1.300 0.21606
## I(x^6) 4.982e-04 4.159e-04 1.198 0.25229
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.501 on 13 degrees of freedom
## Multiple R-squared: 0.8032, Adjusted R-squared: 0.7124
## F-statistic: 8.843 on 6 and 13 DF, p-value: 0.000565532.3.11 嵌套模型的比较
如果两个多元线性回归模型, 第一个模型中的自变量都在第二个模型中, 且第二个模型具有更多的自变量, 则称第一个模型嵌套在第二个模型中。
例如:第一个模型中自变量为\(x_1, x_2, x_5\), 第二个模型自变量为\(x_1, x_2, x_3, x_4, x_5\), 则第一个模型嵌套在第二个模型中。
又如:第一个模型自变量为\(x_1, x_2\), 第二个模型自变量为\(x_1, x_2, x_1^2, x_2^2, x_1 x_2\), 则第一个模型嵌套在第二个模型中。 这时令\(x_3=x_1^2\), \(x_4=x_2^2\), \(x_5=x_1 x_2\), 第二个模型变成有5个自变量的多元线性回归模型。
在嵌套的模型中, 相对而言自变量多的模型叫做完全模型(full model), 自变量少的模型叫做简化模型(reduced model)。
完全模型是否比简化模型更好? 在回归模型选择中贯彻一个“精简性”原则(Ocam’s razor): 在对建模数据拟合效果相近的情况下, 越简单的模型越好。
例如:全模型是 \[ Ey = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_4 x_4 \] 精简模型是 \[ Ey=\beta_0 + \beta_1 x_1 + \beta_2 x_2 \] 判断两个模型是否没有显著差异,只要检验: \[ H_0: \beta_3 = \beta_4 = 0 \] 这可以构造一个方差分析F检验,
设全模型有\(t\)个自变量, 模型得到的回归残差平方和为\(\text{SSE}_f\); 设精简模型有\(s\)个自变量(\(s < t\)), 模型得到的回归残差平方和为\(\text{SSE}_r\); 检验零假设为多出的自变量对应的系数都等于零。 检验统计量为 \[ F = \frac{(\text{SSE}_r - \text{SSE}_f)/(t-s)}{\text{SSE}_f/(n-t-1)} \] 在全模型成立且\(H_0\)成立时,\(F\)服从\(F(t-s, n-t-1)\)分布。 计算右侧p值。
在R中用anova()函数比较两个嵌套的线性回归结果可以进行这样的方差分析F检验。
例如,餐馆营业额回归模型的比较。
lmrst01是完全模型,包含5个自变量;
lmrst02是嵌套的精简模型,
包含居民数、人均餐费、到市中心距离共3个自变量。
用anova()函数可以检验多出的变量是否有意义:
## Analysis of Variance Table
##
## Model 1: 营业额 ~ 居民数 + 人均餐费 + 月收入 + 餐馆数 + 距离
## Model 2: 营业额 ~ 居民数 + 人均餐费 + 距离
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 19 2153.0
## 2 21 2267.2 -2 -114.17 0.5038 0.6121模型p值为0.61, 在0.05水平下不拒绝多出的月收入和餐馆数的系数全为零的零假设, 两个模型的效果没有显著差异, 应选择更精简的模型。
方差分析检验仅能比较嵌套模型。
对不同模型计算AIC,
取AIC较小的模型,
这可以对非嵌套的模型进行比较选择。
R中用AIC()函数比较两个回归结果的AIC值。
如:
## df AIC
## lmrst01 7 196.3408
## lmrst02 5 193.6325精简模型lmrst02的AIC更小,是更好的模型。
32.3.12 拟合与预测
32.3.12.1 拟合
有了参数最小二乘估计后,对建模用的每个数据点计算 \[ \hat y_i = \hat\beta_0 + \hat\beta_1 x_{i1} + \dots + \hat\beta_p x_{ip} \] 称为拟合值(fitted value)。
得到回归模型结果lmres后,要对原数据框中的观测值做预测,
只要使用predict(lmres)。
32.3.12.2 点预测
为了使用得到的模型结果lmres对新数据做预测,
建立包含了自变量的一组新的观测值的数据框dp,
用predict(lmres, newdata=dp)做预测。
如餐馆营业额的选择自变量的回归模型lmrst02的拟合值:
## 1 2 3 4 5 6 7
## 52.1892541 -4.5010247 21.9626575 65.1136964 6.1284803 22.4083426 1.2783244
## 8 9 10 11 12 13 14
## 34.7189934 10.6275869 37.8433996 62.8524888 18.2959990 -5.5101343 14.9558131
## 15 16 17 18 19 20 21
## 8.8598588 29.8309866 78.0159456 13.1673581 15.8469287 50.7274217 27.4608977
## 22 23 24 25
## 0.2331759 22.6274030 48.9610796 27.0050675如果是一元回归,一般还画数据的散点图并画回归直线。 多元回归的图形无法在二维表现出来。
有了估计的回归方程后, 对一组新的自变量值\((x_{01}, \dots, x_{0p})\), 可以计算对应的因变量的预测值: \[ \hat y_0 = \hat\beta_0 + \hat\beta_1 x_{01} + \dots + \hat\beta_p x_{0p} \]
在R中,设lmres保存了回归结果,
newd是一个保存了新的自变量值的数据框,
此数据框结构与原建模用数据框类似但是自变量与原来不同,
且不需要有因变量。
这时用predict(lm1, data=newd)预测。
例如,利用包含居民数、人均餐费、到市中心距离的模型lmrst02,
求居民数=50(万居民),人均餐费=100(元),
距市中心10千米的餐馆的日均营业额:
## 1
## 17.88685预测的日均营业额为17.9千元。
函数expand.grid()可以对若干个变量的指定值,
生成包含所有组合的数据框,如:
## 居民数 人均餐费 距离
## 1 60 50 6
## 2 140 50 6
## 3 60 130 6
## 4 140 130 6
## 5 60 50 16
## 6 140 50 16
## 7 60 130 16
## 8 140 130 16## 1 2 3 4 5 6 7 8
## 14.186636 29.404103 26.797108 42.014574 8.488759 23.706225 21.099230 36.31669632.3.12.3 均值的置信区间
对\(Ey=\beta_0 + \beta_1 x_1 + \dots + \beta_p x_p\), 可以计算置信度为\(1-\alpha\)的置信区间, 称为均值的置信区间。
在predict()中加选项interval="confidence",
用level=指定置信度,
可以计算均值的置信区间。
如
predict(
lmrst02, interval="confidence", level=0.95,
newdata=data.frame(
`居民数`=50, `人均餐费`=100, `距离`=10
))## fit lwr upr
## 1 17.88685 10.98784 24.78585其中fit是预测值,lwr和upr分别是置信下限和置信上限。
32.3.12.4 个别值的预测区间
对\(y=\beta_0 + \beta_1 x_1 + \dots + \beta_p x_p + \varepsilon\), 可以计算置信度为\(1-\alpha\)的预测区间, 称为预测区间,预测区间比均值的置信区间要宽。
在predict()中加选项interval="prediction",
用level=指定置信度,
可以计算预测区间。
如
predict(
lmrst02, interval="prediction", level=0.95,
newdata=data.frame(
`居民数`=50, `人均餐费`=100, `距离`=10
))## fit lwr upr
## 1 17.88685 -4.795935 40.56963其中fit是预测值,lwr和upr分别是预测下限和预测上限。
32.3.13 利用线性回归模型做曲线拟合
某些非线性关系可以通过对因变量和自变量的简单变换变成线性回归模型。
例如, 彩色显影中, 染料光学密度\(Y\)与析出银的光学密度\(x\) 有如下类型的关系 \[ Y \approx A e^{-B/x}, \quad B > 0 \] 这不是线性关系。两边取对数得 \[ \ln Y \approx \ln A - B \frac{1}{x} \] 令 \[ Y^* = \ln Y, \qquad x^* = \frac{1}{x} \] 则 \[ Y^* \approx \ln A - B x^* \] 为线性关系。
从\(n\)组数据 \((x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\)得到变换的数据 \((x_1^*, y_1^*), (x_2^*, y_2^*), \dots, (x_n^*, y_n^*)\)。 对变换后的数据建立线性回归方程 \[\hat y^* = \hat a + \hat b x^*\] 反变换得 \[\hat A = e^{\hat a}, \qquad \hat B = -b\] 则有 \[\hat Y = \hat A e^{-\hat B / x}\]
再考虑一个钢包容积的例子。 炼钢钢包随使用次数增加而容积增大。 测量了13组这样的数据:
SteelBag <- data.frame(
x = c(2, 3, 4, 5, 7, 8, 10,
11, 14, 15, 16, 18, 19),
y = c(106.42, 108.20, 109.58, 109.50, 110.0,
109.93, 110.49, 110.59, 110.60, 110.90,
110.76, 111.00, 111.20)
)| x | y |
|---|---|
| 2 | 106.42 |
| 3 | 108.20 |
| 4 | 109.58 |
| 5 | 109.50 |
| 7 | 110.00 |
| 8 | 109.93 |
| 10 | 110.49 |
| 11 | 110.59 |
| 14 | 110.60 |
| 15 | 110.90 |
| 16 | 110.76 |
| 18 | 111.00 |
| 19 | 111.20 |
散点图:
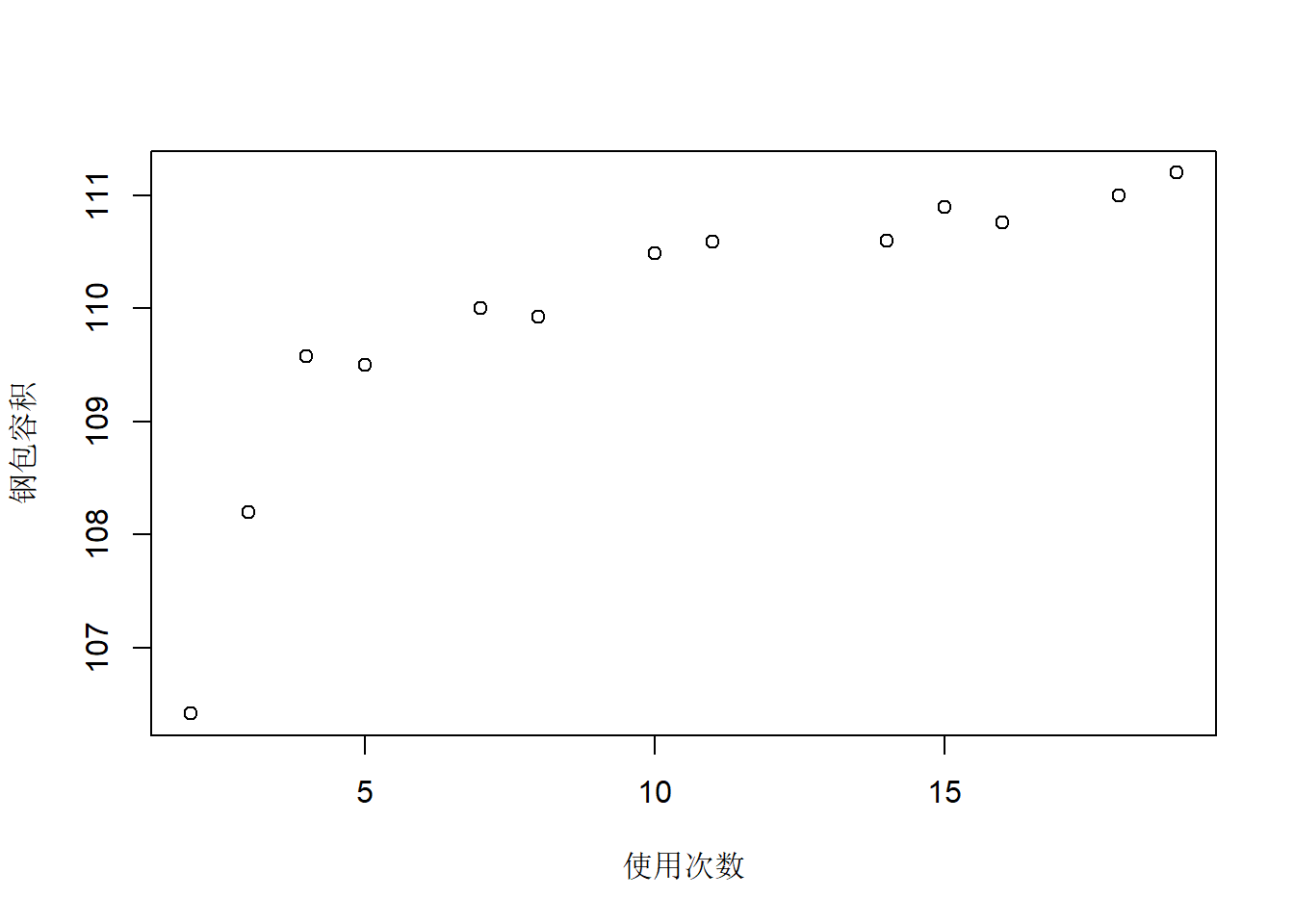
散点图呈现非线性。 用线性回归近似:
##
## Call:
## lm(formula = y ~ x, data = SteelBag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.97615 -0.38502 0.04856 0.53724 0.80611
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 108.01842 0.44389 243.346 < 2e-16 ***
## x 0.18887 0.03826 4.937 0.000445 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7744 on 11 degrees of freedom
## Multiple R-squared: 0.689, Adjusted R-squared: 0.6607
## F-statistic: 24.37 on 1 and 11 DF, p-value: 0.000445结果显著。 \(R^2=0.69\)。 拟合图:
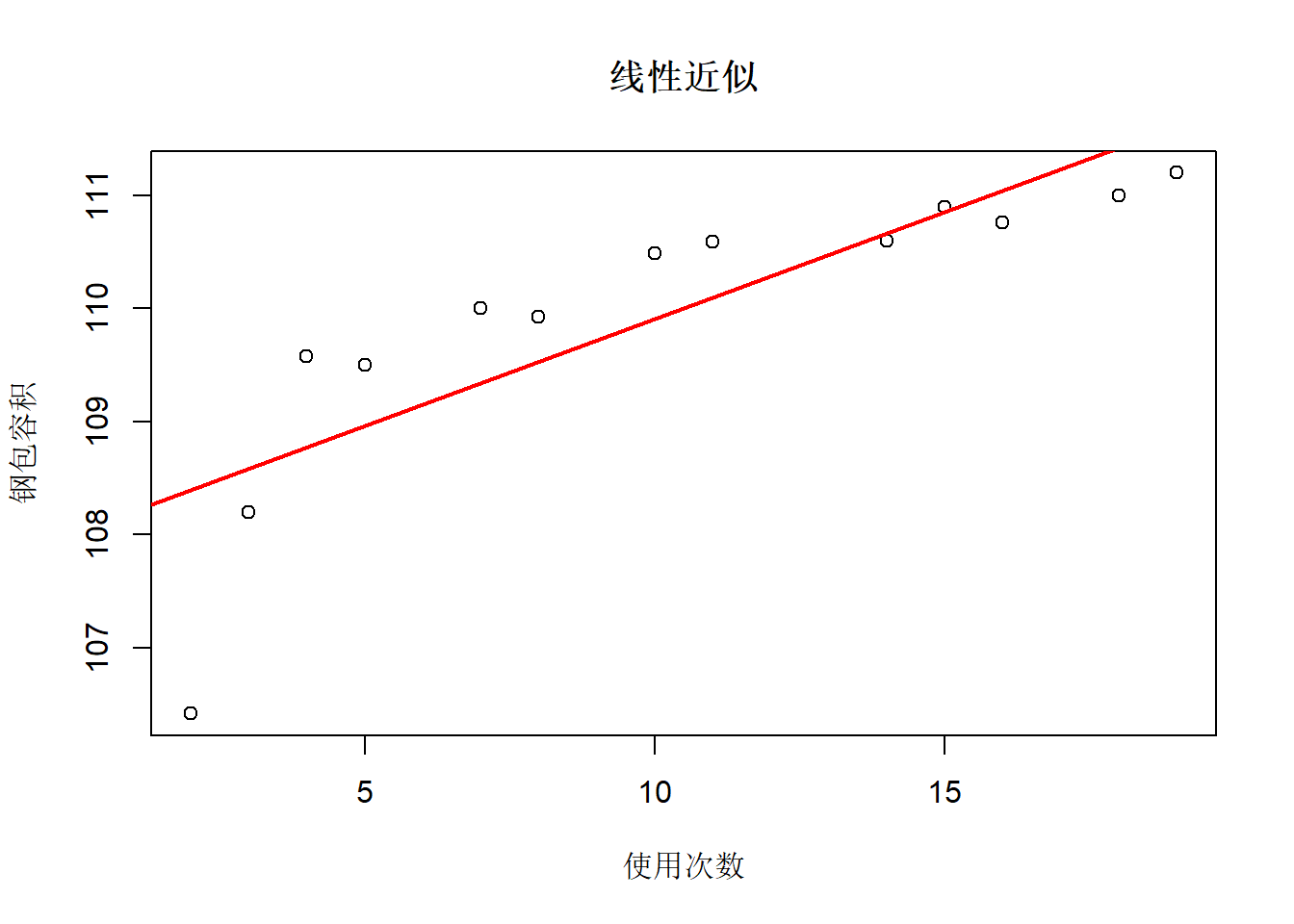
残差诊断:
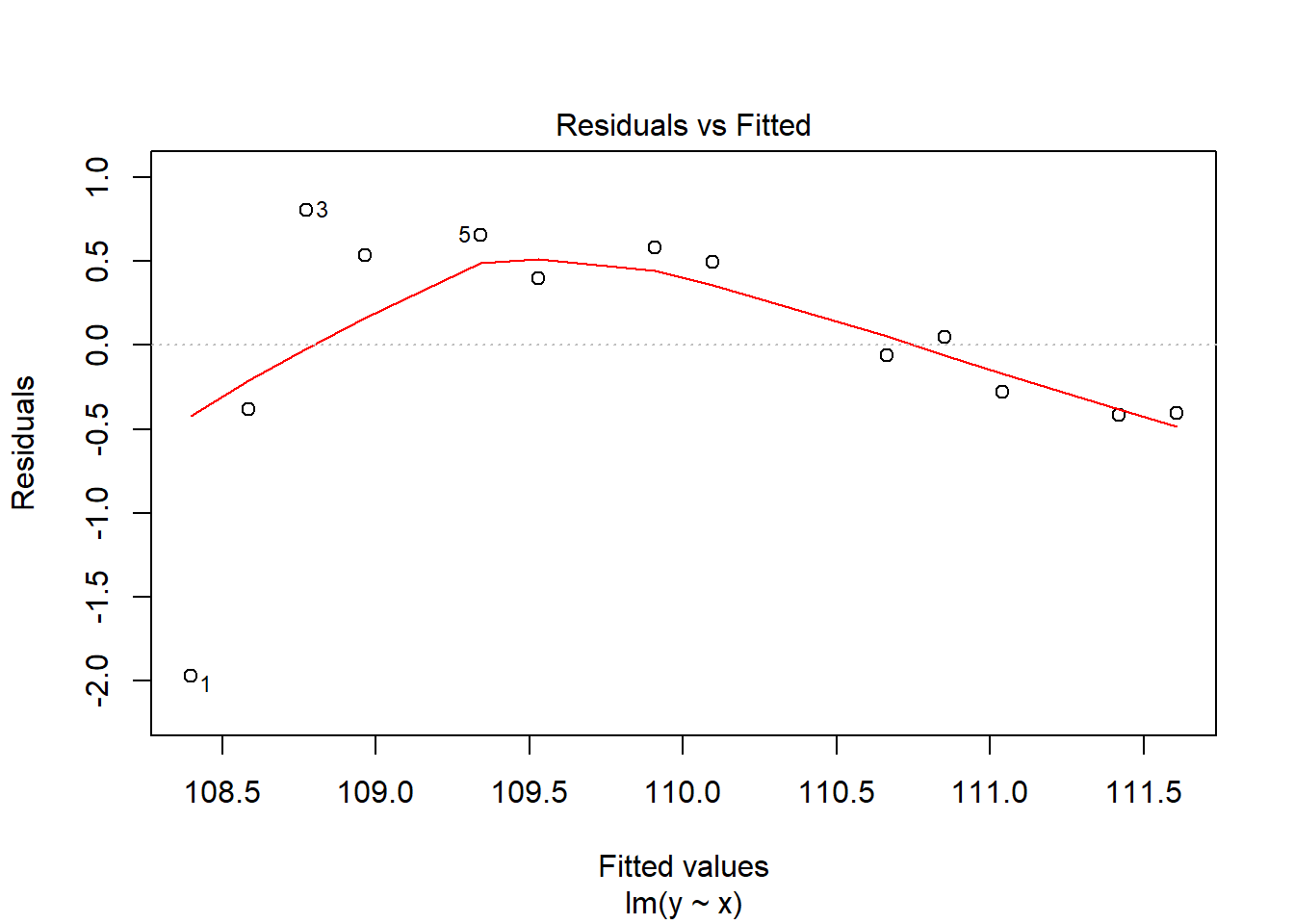
残差图呈现非线性。
用双曲线模型: \[ \frac{1}{y} \approx a + b \frac{1}{x} \]
令\(x^* = 1/x, y^* = 1/y\),化为线性模型 \[y^* \approx a + b x^*\]
\((x^*, y^*)\)的散点图:
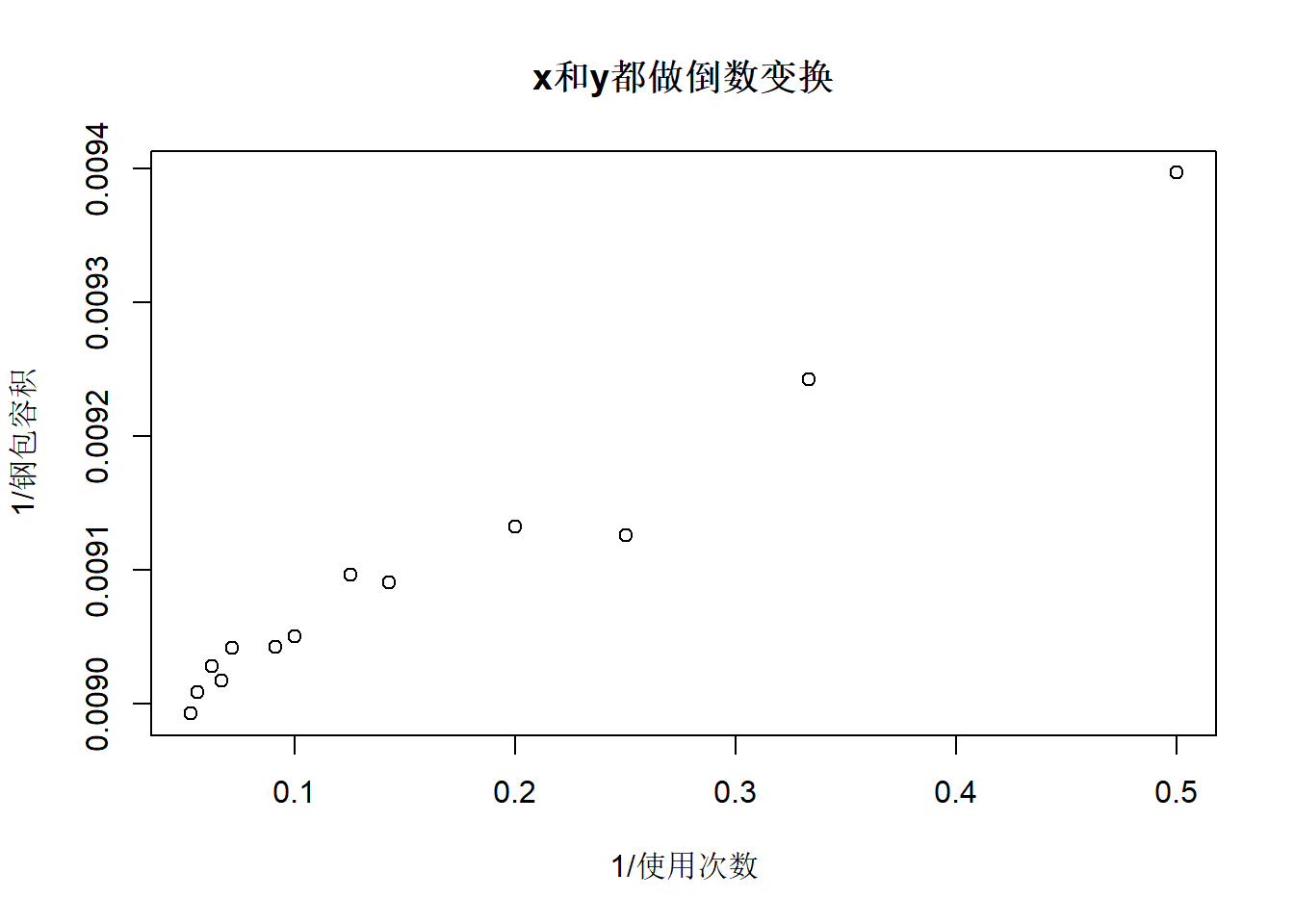
\(y^*\)对\(x^*\)的回归:
##
## Call:
## lm(formula = I(1/y) ~ I(1/x), data = SteelBag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.817e-05 -3.686e-06 4.000e-07 1.008e-05 2.642e-05
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 8.967e-03 8.371e-06 1071.14 < 2e-16 ***
## I(1/x) 8.292e-04 4.118e-05 20.14 4.97e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.903e-05 on 11 degrees of freedom
## Multiple R-squared: 0.9736, Adjusted R-squared: 0.9712
## F-statistic: 405.4 on 1 and 11 DF, p-value: 4.97e-10结果显著。 解得\(\hat a = 0.008967\), \(\hat b = 0.0008292\), 经验公式为 \[ \frac{1}{\hat y} = 0.008967 + 0.0008292 \frac{1}{x} \] \(R^2\)从线性近似的0.69提高到了0.97。
拟合图:
with(SteelBag, plot(
x, y, xlab="使用次数", ylab="钢包容积",
main="线性和非线性回归"
))
abline(lmsb1, col="red", lwd=2)
curve(1/(0.008967 + 0.0008292/x), 1, 20,
col="green", lwd=2, add=TRUE)
legend("bottomright", lty=1, lwd=2,
col=c("red", "green"),
legend=c("线性回归", "曲线回归"))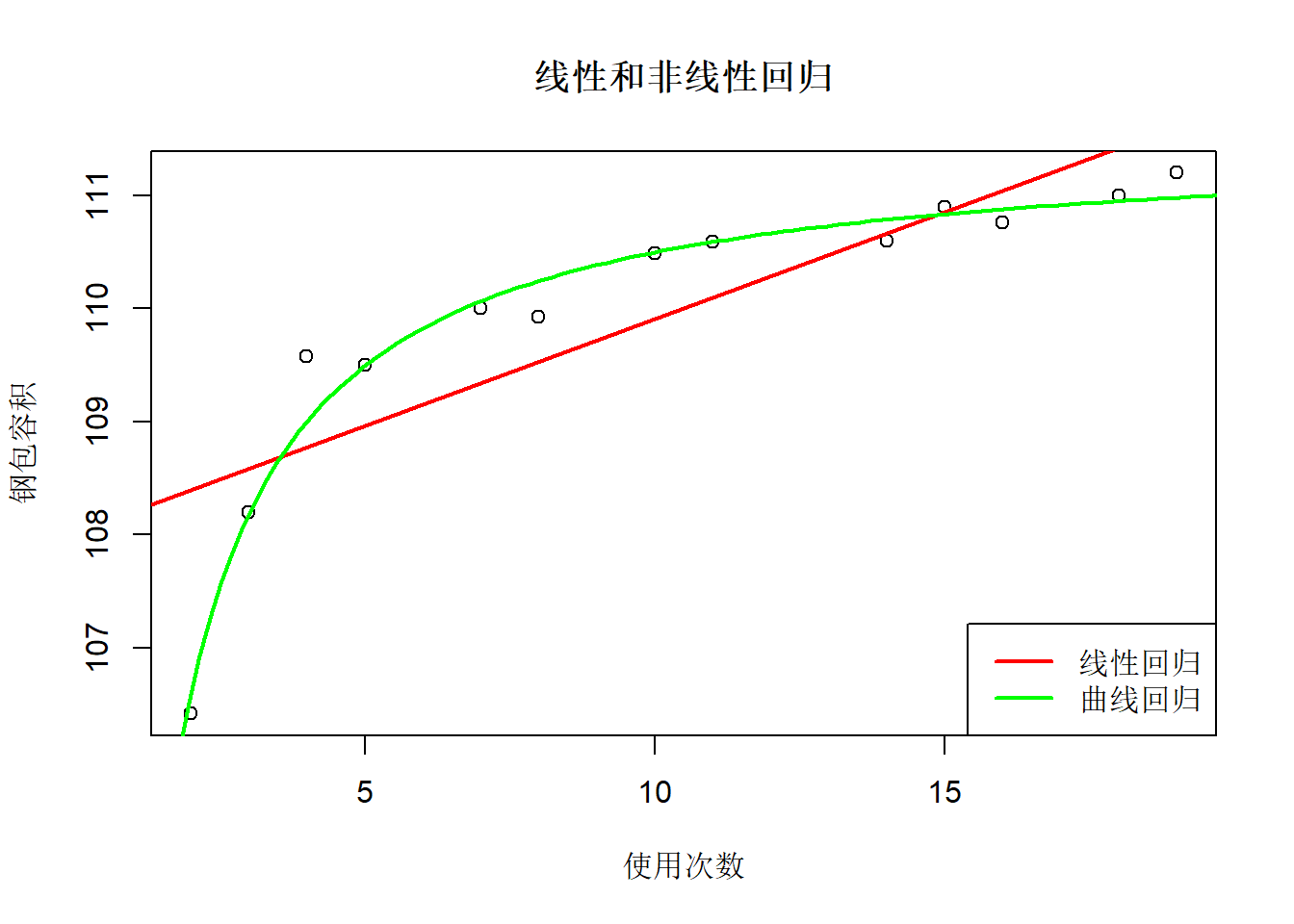
考虑Reynolds, Inc.销售业绩数据分析问题。 Reynolds, Inc.是一个工业和试验室量具厂商。 为研究销售业务员的业绩, 考察业务员从业年限(Months, 单位:月)与其销售的电子量具数量(Sales)的关系。 随机抽查了15名业务员。
| Months | Sales |
|---|---|
| 41 | 275 |
| 106 | 296 |
| 76 | 317 |
| 104 | 376 |
| 22 | 162 |
| 12 | 150 |
| 85 | 367 |
| 111 | 308 |
| 40 | 189 |
| 51 | 235 |
| 9 | 83 |
| 12 | 112 |
| 6 | 67 |
| 56 | 325 |
| 19 | 189 |
散点图:

散点图呈现非线性。
用线性近似:
##
## Call:
## lm(formula = Sales ~ Months, data = Reynolds)
##
## Residuals:
## Min 1Q Median 3Q Max
## -67.166 -38.684 2.557 28.875 80.673
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 111.2279 21.6280 5.143 0.000189 ***
## Months 2.3768 0.3489 6.812 1.24e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 49.52 on 13 degrees of freedom
## Multiple R-squared: 0.7812, Adjusted R-squared: 0.7643
## F-statistic: 46.41 on 1 and 13 DF, p-value: 1.239e-05结果显著。 \(R^2=0.78\)。 拟合图:
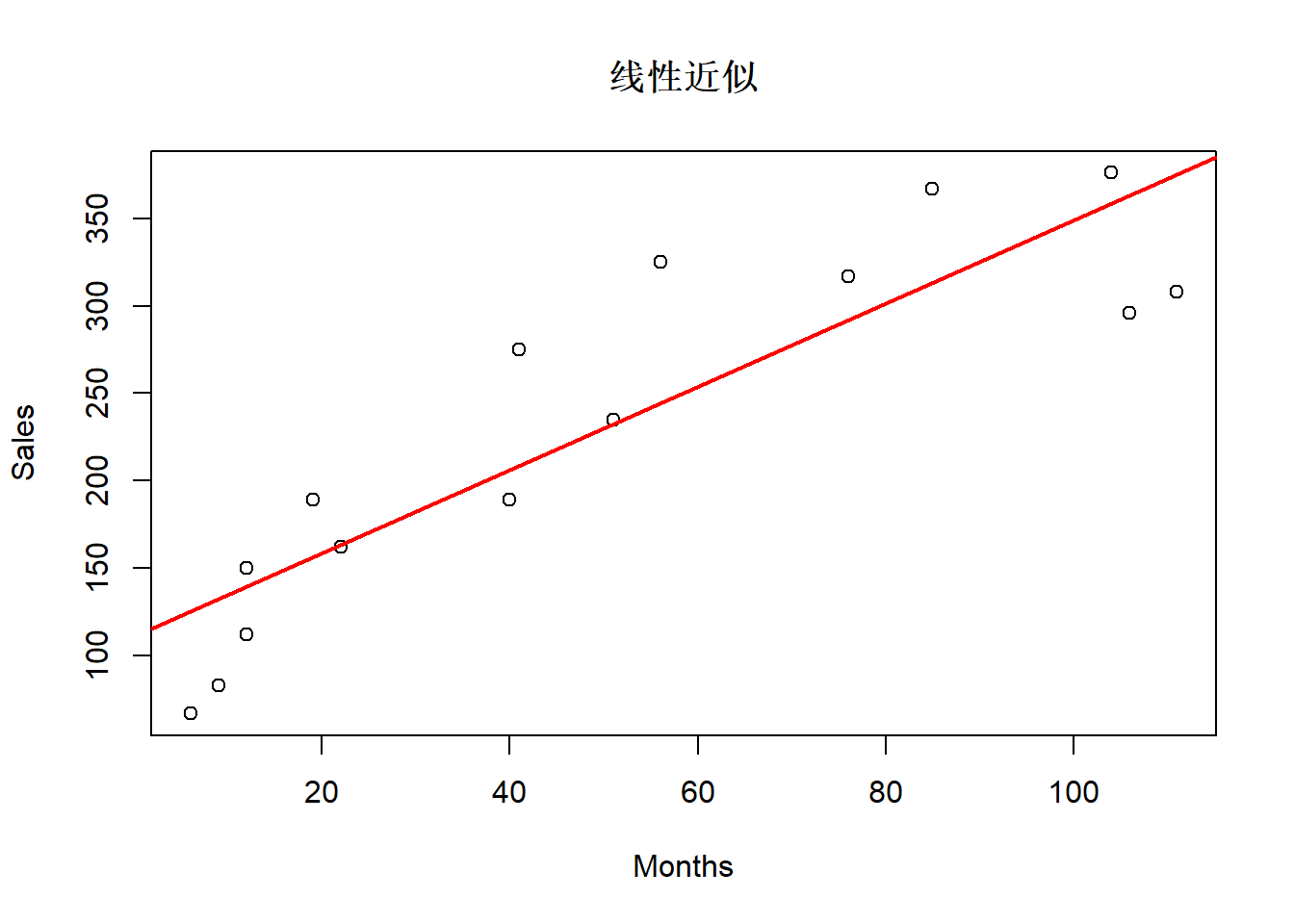
残差诊断:
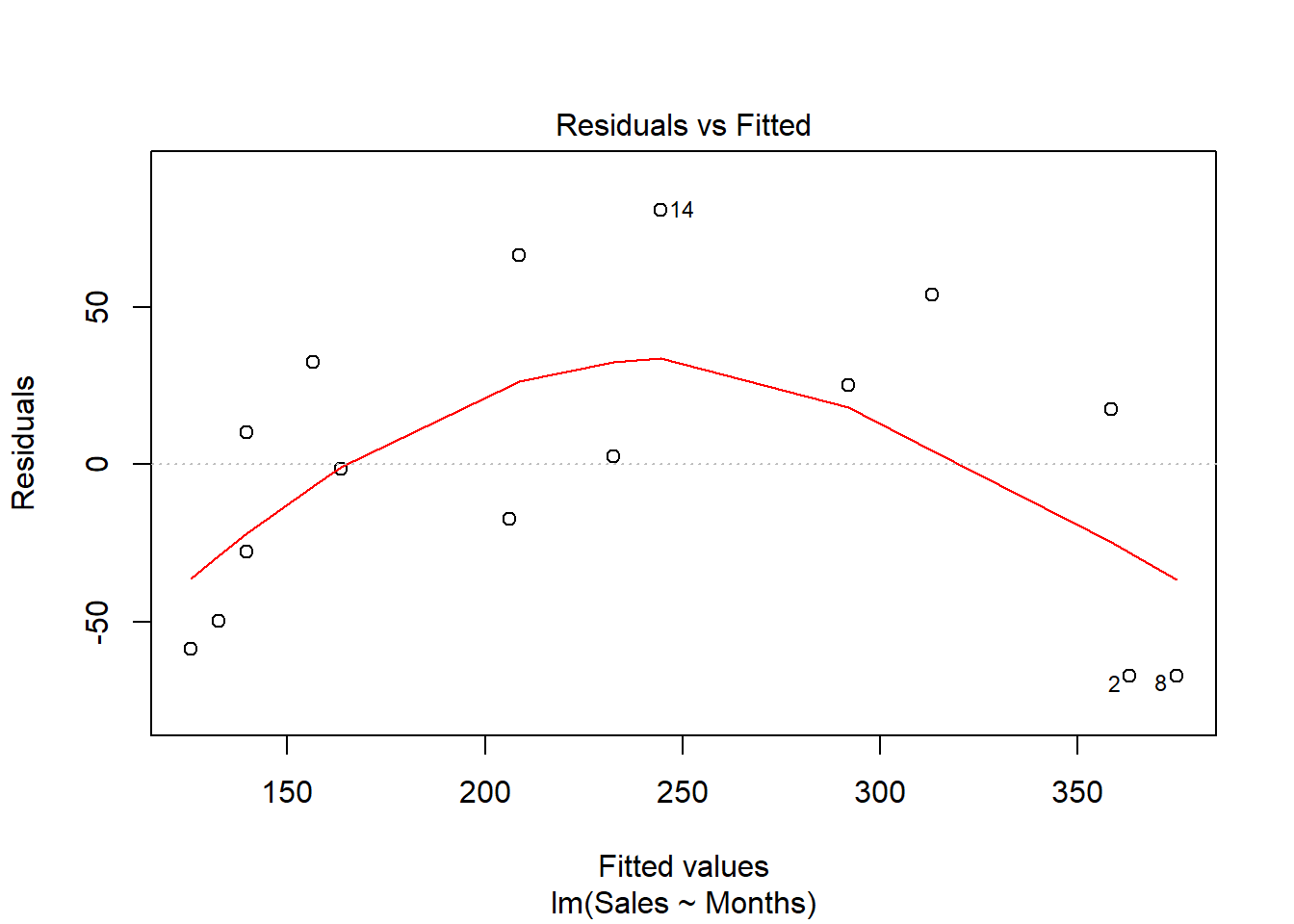
残差图有明显的非线性。
考虑最简单的非线性模型: \[ y = \beta_0 + \beta_1 x + \beta_2 x^2 + \varepsilon \] 令\(x_1 = x\), \(x_2=x^2\),有 \[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \varepsilon \] 是二元线性回归模型。 作二次多项式回归:
##
## Call:
## lm(formula = Sales ~ Months + I(Months^2), data = Reynolds)
##
## Residuals:
## Min 1Q Median 3Q Max
## -54.963 -16.691 -6.242 31.996 43.789
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 45.347579 22.774654 1.991 0.06973 .
## Months 6.344807 1.057851 5.998 6.24e-05 ***
## I(Months^2) -0.034486 0.008948 -3.854 0.00229 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 34.45 on 12 degrees of freedom
## Multiple R-squared: 0.9022, Adjusted R-squared: 0.8859
## F-statistic: 55.36 on 2 and 12 DF, p-value: 8.746e-07模型显著。 \(R^2\)从线性近似的0.78提高到0.90。 \(x^2\)项的系数的显著性检验p值为0.002,显著不等于零, 说明二次项是必要的。
这样添加二次项容易造成\(x\)与\(x^2\)之间的共线性, 所以添加中心化的二次项: \[x_2 = (x - 60)^2\]
##
## Call:
## lm(formula = Sales ~ Months + I((Months - 60)^2), data = Reynolds)
##
## Residuals:
## Min 1Q Median 3Q Max
## -54.963 -16.691 -6.242 31.996 43.789
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 169.495742 21.331978 7.946 4.03e-06 ***
## Months 2.206535 0.246744 8.943 1.18e-06 ***
## I((Months - 60)^2) -0.034486 0.008948 -3.854 0.00229 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 34.45 on 12 degrees of freedom
## Multiple R-squared: 0.9022, Adjusted R-squared: 0.8859
## F-statistic: 55.36 on 2 and 12 DF, p-value: 8.746e-07with(Reynolds, plot(Months, Sales, main="线性和非线性回归"))
abline(lmre1, col="red", lwd=2)
curve(196.50 + 2.2065*x - 0.03449*(x-60)^2, 5, 110,
col="green", lwd=2, add=TRUE)
legend("bottomright", lty=1, lwd=2,
col=c("red", "green"),
legend=c("线性回归", "曲线回归"))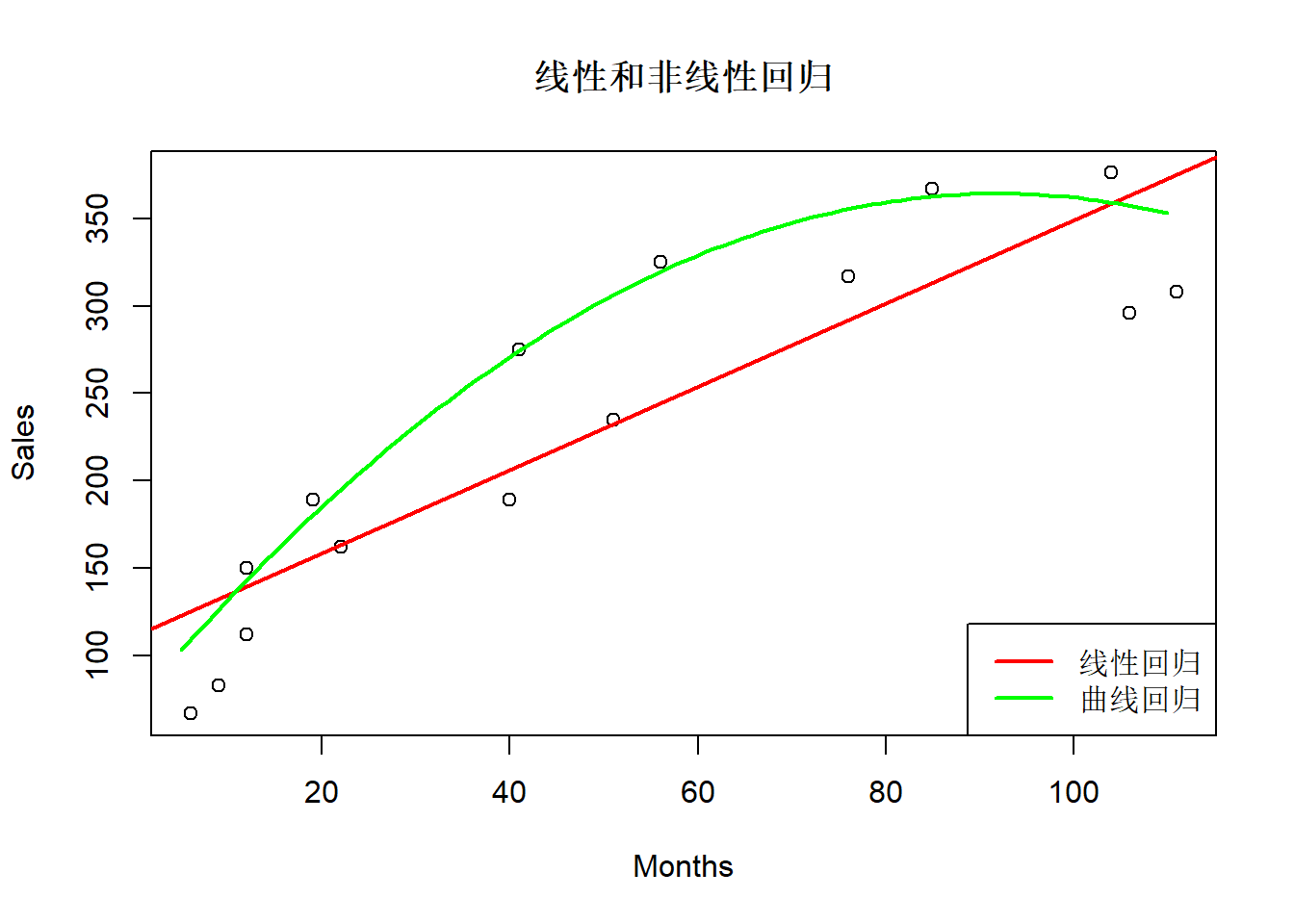
32.3.14 分组建立多个模型
有时希望将数据按照一个或者几个分类变量分组,
每一组分别建立模型,
并将模型结果统一列表比较。
broom包可以用来将模型结果转换成规范的数据框格式。
以肺癌病人数据为例,
建立v1对v0和age的多元线性回归模型:
## # A tibble: 34 x 6
## id age sex type v0 v1
## <dbl> <dbl> <chr> <chr> <dbl> <dbl>
## 1 1 70 F 腺癌 26.5 2.91
## 2 2 70 F 腺癌 135. 35.1
## 3 3 69 F 腺癌 210. 74.4
## 4 4 68 M 腺癌 61 35.0
## 5 5 67 M 鳞癌 238. 128.
## 6 6 75 F 腺癌 330. 112.
## 7 7 52 M 鳞癌 105. 32.1
## 8 8 71 M 鳞癌 85.2 29.2
## 9 9 68 M 鳞癌 102. 22.2
## 10 10 79 M 鳞癌 65.5 21.9
## # ... with 24 more rows##
## Call:
## lm(formula = v1 ~ v0 + age, data = d.cancer)
##
## Residuals:
## Min 1Q Median 3Q Max
## -42.757 -11.010 -2.475 11.907 52.941
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.90818 33.14895 0.239 0.814
## v0 0.43288 0.05564 7.780 1.79e-07 ***
## age -0.12846 0.53511 -0.240 0.813
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 21.76 on 20 degrees of freedom
## (11 observations deleted due to missingness)
## Multiple R-squared: 0.7683, Adjusted R-squared: 0.7451
## F-statistic: 33.16 on 2 and 20 DF, p-value: 4.463e-07用broom包的tidy()函数可以将系数估计结果转换成合适的tibble数据框格式:
## Warning: 程辑包'broom'是用R版本3.6.3 来建造的## # A tibble: 3 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 7.91 33.1 0.239 0.814
## 2 v0 0.433 0.0556 7.78 0.000000179
## 3 age -0.128 0.535 -0.240 0.813用broom包的augment()函数可以获得拟合值、残差等每个观测的回归结果:
| .rownames | v1 | v0 | age | .fitted | .se.fit | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.91 | 26.51 | 70 | 10.39 | 7.92 | -7.48 | 0.13 | 22.25 | 0.01 | -0.37 |
| 2 | 35.08 | 135.48 | 70 | 57.56 | 5.43 | -22.48 | 0.06 | 21.68 | 0.03 | -1.07 |
| 3 | 74.44 | 209.74 | 69 | 89.84 | 6.92 | -15.40 | 0.10 | 22.01 | 0.02 | -0.75 |
| 4 | 34.97 | 61.00 | 68 | 25.58 | 6.06 | 9.39 | 0.08 | 22.21 | 0.01 | 0.45 |
| 5 | 128.34 | 237.75 | 67 | 102.22 | 8.06 | 26.12 | 0.14 | 21.37 | 0.09 | 1.29 |
| 6 | 112.34 | 330.24 | 75 | 141.23 | 12.50 | -28.89 | 0.33 | 20.81 | 0.43 | -1.62 |
| 7 | 32.10 | 104.90 | 52 | 46.64 | 7.83 | -14.54 | 0.13 | 22.04 | 0.03 | -0.72 |
| 8 | 29.15 | 85.15 | 71 | 35.65 | 6.31 | -6.50 | 0.08 | 22.27 | 0.00 | -0.31 |
| 9 | 22.15 | 101.65 | 68 | 43.18 | 5.10 | -21.03 | 0.05 | 21.77 | 0.02 | -0.99 |
| 10 | 21.94 | 65.54 | 79 | 26.13 | 10.19 | -4.19 | 0.22 | 22.30 | 0.00 | -0.22 |
| 11 | 12.33 | 125.31 | 55 | 55.09 | 6.88 | -42.76 | 0.10 | 19.79 | 0.16 | -2.07 |
| 12 | 99.44 | 224.36 | 54 | 98.09 | 10.54 | 1.35 | 0.23 | 22.32 | 0.00 | 0.07 |
| 13 | 2.30 | 12.93 | 55 | 6.44 | 7.58 | -4.14 | 0.12 | 22.30 | 0.00 | -0.20 |
| 14 | 23.96 | 40.21 | 75 | 15.68 | 9.24 | 8.28 | 0.18 | 22.23 | 0.01 | 0.42 |
| 15 | 7.39 | 12.58 | 61 | 5.52 | 6.93 | 1.87 | 0.10 | 22.32 | 0.00 | 0.09 |
| 16 | 112.58 | 231.04 | 76 | 98.16 | 8.81 | 14.42 | 0.16 | 22.03 | 0.03 | 0.72 |
| 17 | 91.62 | 172.13 | 65 | 74.07 | 5.57 | 17.55 | 0.07 | 21.93 | 0.02 | 0.83 |
| 18 | 13.95 | 39.26 | 66 | 16.42 | 6.37 | -2.47 | 0.09 | 22.32 | 0.00 | -0.12 |
| 20 | 122.45 | 161.00 | 63 | 69.51 | 5.43 | 52.94 | 0.06 | 18.47 | 0.14 | 2.51 |
| 21 | 68.35 | 105.26 | 67 | 44.87 | 4.84 | 23.48 | 0.05 | 21.63 | 0.02 | 1.11 |
| 22 | 5.25 | 13.25 | 51 | 7.09 | 8.67 | -1.84 | 0.16 | 22.32 | 0.00 | -0.09 |
| 23 | 3.34 | 18.70 | 49 | 9.71 | 9.27 | -6.37 | 0.18 | 22.27 | 0.01 | -0.32 |
| 24 | 50.36 | 60.23 | 49 | 27.69 | 8.91 | 22.67 | 0.17 | 21.59 | 0.09 | 1.14 |
用broom包的glance()函数可以将回归的复相关系数平方、F检验p值等整体结果做成一行的数据框:
| r.squared | adj.r.squared | sigma | statistic | p.value | df | logLik | AIC | BIC | deviance | df.residual |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.77 | 0.75 | 21.76 | 33.16 | 0 | 3 | -101.87 | 211.74 | 216.28 | 9470.34 | 20 |
下面将男病人与女病人分别建模,
并以表格形式合并分组的建模结果。
用dplyr包的group_by()函数分组,
用tidyr包的nest()函数可以将分组后的数据框转换成一个新的数据框,
新数据框中有一列是列表类型,
每个元素是一个子数据框:
## # A tibble: 2 x 2
## # Groups: sex [2]
## sex data
## <chr> <list>
## 1 F <tibble [13 x 5]>
## 2 M <tibble [21 x 5]>这样,
可以用purr::map()函数对每一组分别建模,
建模结果可以借助broom包制作成合适的数据框格式,
然后用unnest()函数将不同组的结果合并成一个大数据框,如:
d.cancer %>%
group_by(sex) %>%
nest() %>%
mutate(model = map(data, function(df) summary(lm(v1 ~ v0 + age, data=df))),
tidied = map(model, tidy)) %>%
unnest(tidied, .drop = TRUE)## Warning: The `.drop` argument of `unnest()` is deprecated as of tidyr 1.0.0.
## All list-columns are now preserved.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_warnings()` to see where this warning was generated.## # A tibble: 6 x 8
## # Groups: sex [2]
## sex data model term estimate std.error statistic p.value
## <chr> <list> <list> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 F <tibble [13 x~ <smmry.~ (Interce~ 171. 147. 1.16 3.10e-1
## 2 F <tibble [13 x~ <smmry.~ v0 0.485 0.136 3.56 2.35e-2
## 3 F <tibble [13 x~ <smmry.~ age -2.74 2.39 -1.15 3.16e-1
## 4 M <tibble [21 x~ <smmry.~ (Interce~ -17.2 30.5 -0.563 5.83e-1
## 5 M <tibble [21 x~ <smmry.~ v0 0.486 0.0657 7.39 5.28e-6
## 6 M <tibble [21 x~ <smmry.~ age 0.204 0.484 0.421 6.81e-1当需要分组拟合许多个模型时, 这种方法比较方便。
32.4 非参数回归
32.4.1 模型
线性回归模型可以看成非线性回归模型的特例: \[Y = f(X) + \varepsilon\] 其中\(f(x)\)为未知的回归函数。
参数方法:假定\(f(x)\)具有某种形式,如
- \(f(x) = a + b x\): 线性回归;
- \(f(x) = a + b x + c x^2\): 二次多项式回归;
- \(f(x) = A e^{bx}\): 指数模型,等等。
二次多项式回归可以令\(X_1 = x, X_2 = x^2\), 变成二元回归模型来解决。 指数模型可以令\(z = \ln Y\), 模型化为\(z = a + bx\)。 有一些曲线模型可以通过变换化为线性回归。
在多元情形, 一般的非线性回归模型为 \[ Y = f(x_1, x_2, \dots, x_p) + \varepsilon \] 但是这样可选的模型就过于复杂, 难以把握。 比较简单的是不考虑变量之间交互作用的可加模型:
\[ Y = \sum_{j=1}^p f_j(x_j) + \varepsilon \] 其中\(f_j(\cdot)\)是未知的回归函数, 需要满足一定的光滑性条件。
\(f_j(\cdot)\)可以是参数形式的, 比如二次多项式、三次多项式、阶梯函数等。 较好的一种选择是使用三次样条函数。
32.4.2 样条平滑
为了得到一般性的\(Y\)与\(X\)的曲线关系\(f(x)\)的估计, 可以使用样条函数。 三次样条函数将实数轴用若干个节点(knots) \(\{ z_k \}\)分成几段, 每一段上\(\hat f(x)\)为三次多项式, 函数在节点处有连续的二阶导数。 样条函数是光滑的分段三次多项式。
用样条函数估计\(f(x)\)的准则是曲线接近各观测值点 \((x_i, y_i)\),同时曲线足够光滑。
在R中用smooth.spline函数进行样条曲线拟合。
取每个自变量\(x_i\)处为一个节点,
对于给定的某个光滑度/模型复杂度系数值\(\lambda\),
求函数\(f(x)\)使得
\[
\min_{f(\cdot)}
\left\{
\sum_i [y_i - f(x_i)]^2 + \lambda \int [f''(x)]^2 \,dx
\right\}
\]
\(\lambda\)越大,
所得的曲线越光滑。
smooth.spline()函数可以通过交叉验证方法自动取得一个对于预测最优的光滑参数\(\lambda\)值,
也可以通过df=选项指定一个等效自由度,
等效自由度越大,
模型越复杂,
曲线光滑程度越低。
df值相当于多元线性回归中的自变量个数。
如
set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
xx <- seq(-10, 10, length.out=100)
x <- sort(x)
y <- 10*sin(x/10*pi)^2 + rnorm(nsamp,0,0.3)
plot(x, y)
curve(10*sin(x/10*pi)^2, -10, 10, add=TRUE, lwd=2)
library(splines)
res <- smooth.spline(x, y)
lines(spline(x, res$y), col="red")
res2 <- loess(y ~ x, degree=2, span=0.3)
lines(xx, predict(res2, newdata=data.frame(x=xx)),
col="blue")
legend("top", lwd=c(2,1,1),
col=c("black", "red", "blue"),
legend=c("真实函数关系", "样条平滑结果", "局部线性拟合"))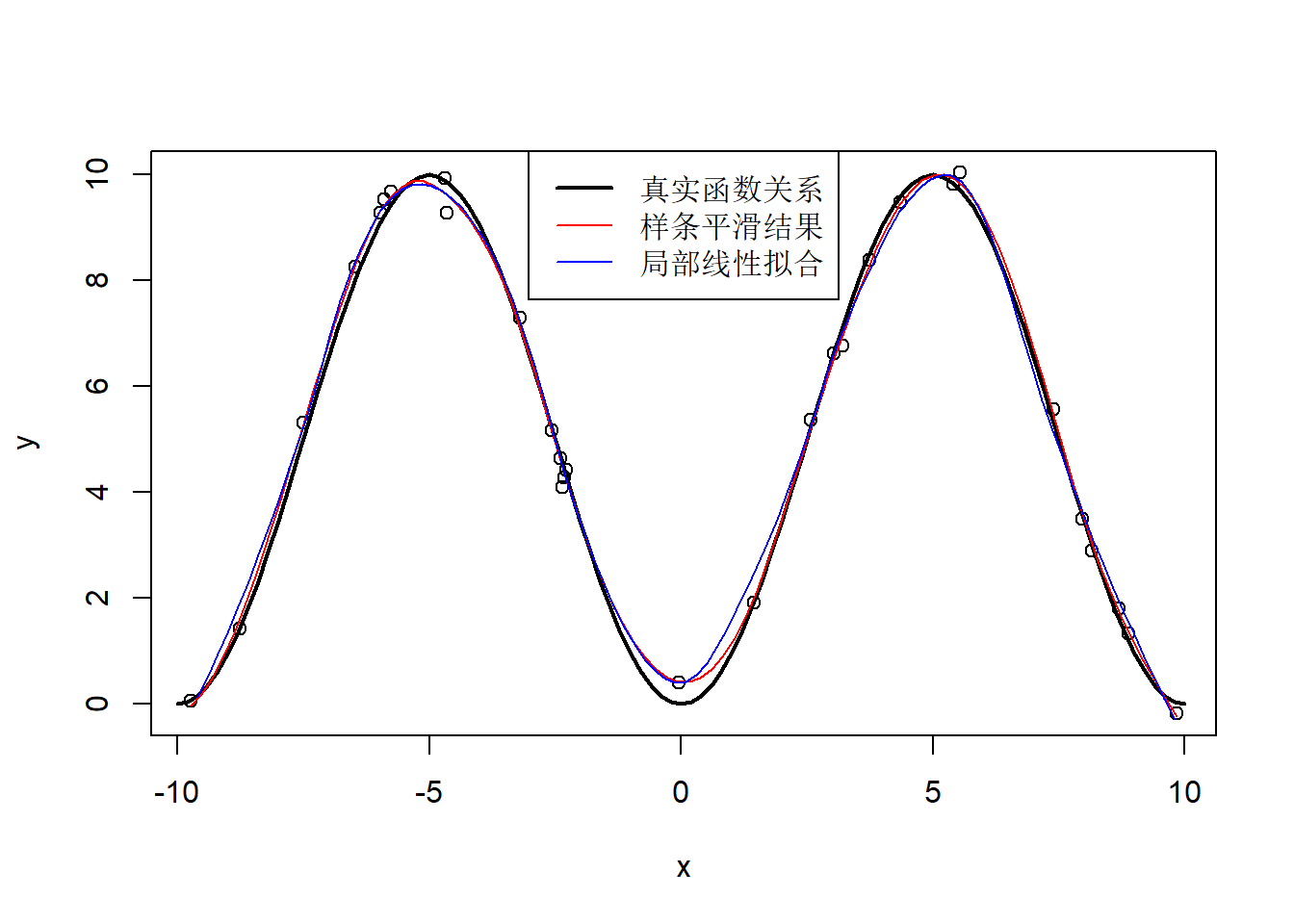
图32.11: 曲线平滑示例
其中res的元素y为拟合值,用spline(x,y)从一组散点输出
光滑曲线以便用lines()函数绘图。
R函数splines(x,y)不是做样条平滑,
而是做样条插值,
其结果是在原始的自变量x范围内产生等间隔距离的格子点值,
输出包含格子点上的样条插值x和y坐标的列表。
样条平滑曲线不需要穿过输入的各个散点,
但是插值则需要穿过输入的各个散点。
R函数approx(x,y)用线性插值方法产生线性插值后的连续函数在等间隔的横坐标上的坐标值。
32.4.3 局部多项式曲线平滑
另一种非参数的拟合非线性回归曲线\(f(x)\)的方法是对每个自变量\(x\) 处选一个局部的小邻域, 用这个小邻域附近的\((x_i, y_i)\)点拟合一个局部的零次、一次或二次多项式, 用拟合的局部多项式在\(x\)处的值作为回归函数在\(x\)处的值的估计。
局部零次多项式的方法叫做核回归, 公式为 \[ \hat f(x) = \frac{\sum\limits_{i = 1}^n {K\left( {\frac{{x - X_i }}{h}} \right)Y_i } } {\sum\limits_{i = 1}^n {K\left( {\frac{{x - X_i }}{h}} \right)} } \] 其中\(K(\cdot)\)称为核函数, 是类似标准正态密度这样的中间高两边低的可以用来加权的函数, 比如, 双三次核函数: \[ K(x) = \left\{ {\begin{array}{*{20}c} {\left( {1 - \left| x \right|^3 } \right)^3 } & {\left| x \right| \leq 1} \\ 0 & \mbox{其它} \\ \end{array}} \right. \]
kernel.dcube <- function(u){
y <- numeric(length(u))
sele <- (abs(u) < 1)
y[sele] <- (1 - abs(u[sele])^3)^3
y
}
curve(kernel.dcube, -1.5, 1.5, main="双三次核函数")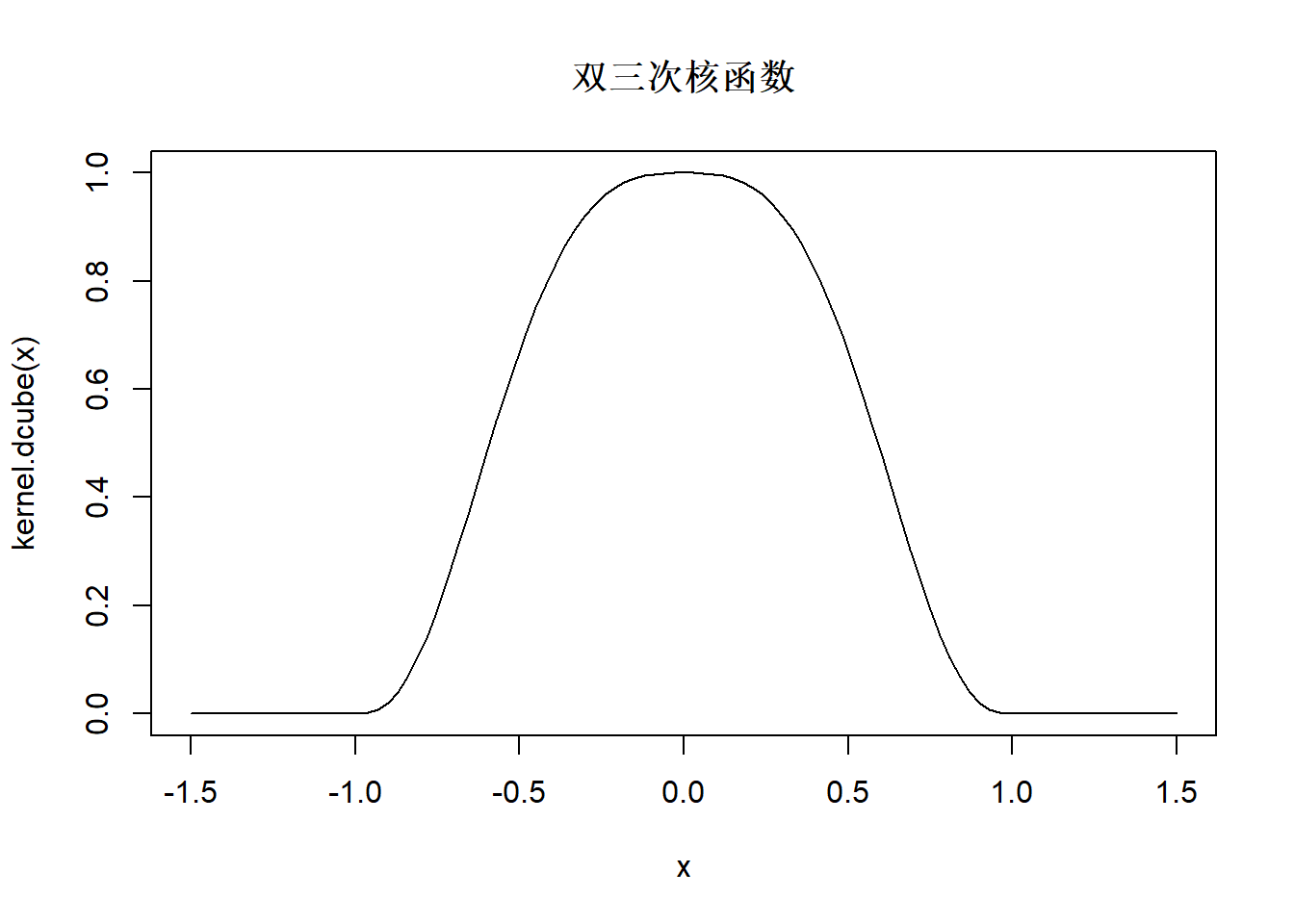
图32.12: 双三次核函数
参数\(h\)称为窗宽, \(h\)越大,参与平均的点越多, 曲线越光滑, 回归复杂度越低。 \(h\)选取可以用交叉验证方法。
R扩展包KernSmooth的函数
locpoly(x, y, degree=1, bandwidth=0.25)可以计算核回归,
其中bandwidth是输入的窗宽,
函数dpill(x,y)可以帮助确定窗宽。
如
locpoly(x, y, degree=1, bandwidth=dpill(x,y))。
stats包的ksmooth()函数也可以计算核回归。
当局部拟合的是一次或者二次多项式时,
这种曲线拟合方法叫做局部多项式回归。
R函数loess(y ~ x, degree=1, span=0.75)拟合局部线性函数,
用span=控制结果的光滑度,
span是局部拟合所用的点的比例,
越接近于1结果越光滑。
取degree=2拟合局部二次多项式函数。
见图32.11。
32.4.4 样条函数变换
\(m\)个节点的三次样条函数需要\(n+4\)个参数, 因为每段需要\(4\)个参数, \(m+1\)段需要\(4m+4\)个参数, 而在\(m\)个节点上连续、一阶导数连续、二阶导数连续构成三个约束条件, 所以参数个数为\(m+4\)个。
自然样条函数假定函数在最左边一段和最右边一段为线性函数,
这样\(m\)个节点需要\(m+2\)个参数。
R的lm()函数中对自变量x指定ns(x)
可以对输入的x指定作自然样条变换,
ns()可以用df=指定自由度作为曲线复杂度的度量。
如
set.seed(1)
nsamp <- 30
x <- runif(nsamp, -10, 10)
xx <- seq(-10, 10, length.out=100)
x <- sort(x)
y <- 10*sin(x/10*pi)^2 + rnorm(nsamp,0,0.3)
plot(x, y)
curve(10*sin(x/10*pi)^2, -10, 10, add=TRUE, lwd=2)
res <- lm(y ~ ns(x, df=4))
lines(xx, predict(res, newdata=data.frame(x=xx)),
col="red")
res2 <- lm(y ~ ns(x, df=8))
lines(xx, predict(res2, newdata=data.frame(x=xx)),
col="blue")
legend("top", lwd=c(2,1,1),
col=c("black", "red", "blue"),
legend=c("真实函数关系", "ns(df=4)", "ns(df=8)"))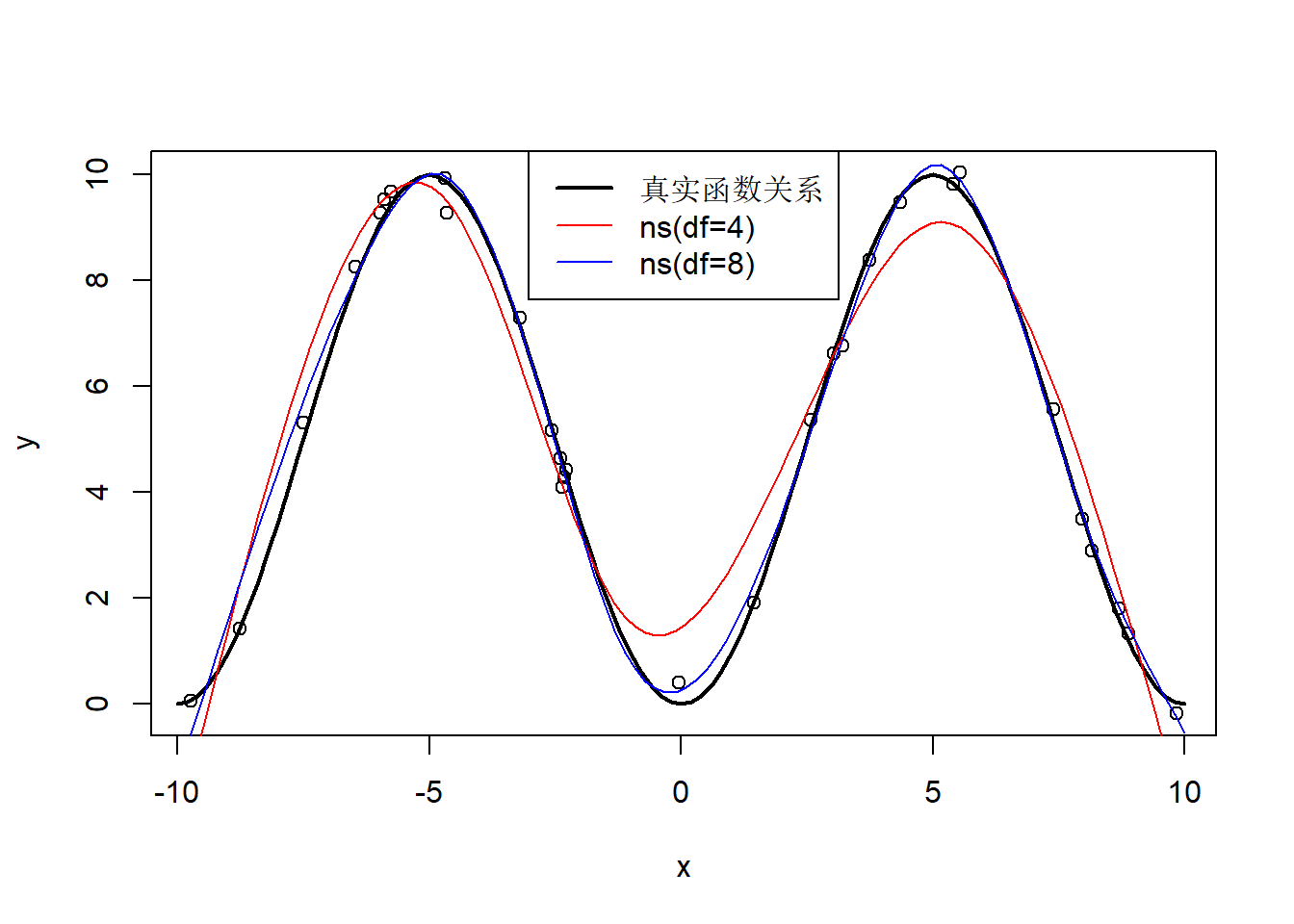
图32.13: 自然样条回归示例
在多元回归中也可以用ns(x)对单个自变量引入非线性。
32.4.5 线性可加模型
虽然在用lm()作多元回归时可以用ns()、poly()等函数引入非线性成分,
但需要指定复杂度参数。
对可加模型
\[
Y = \sum_{j=1}^p f_j(x_j) + \varepsilon
\]
最好能从数据中自动确定\(f_j(\cdot)\)的复杂度(光滑度)参数。
R扩展包mgcv的gam()函数可以执行这样的可加模型的非参数回归拟合。
模型中可以用s(x)指定x的样条平滑,
用lo(x)指定x的局部多项式平滑。
具体的计算是迭代地对每个自变量\(x_j\)进行,
估计\(x_j\)的平滑函数\(f_j(\cdot)\)时,
采用数据\(\tilde y = Y - \sum_{k \neq j} f_k(x_k)\),
迭代估计到结果基本不变为止。
例如,MASS包的rock数据框是石油勘探中12块岩石样本分别产生4个切片得到的测量数据, 共48个观测, 因变量是渗透率(permeability), 自变量为area, peri, shape。
先作线性回归:
##
## Call:
## lm(formula = log(perm) ~ area + peri + shape, data = rock)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.8092 -0.5413 0.1734 0.6493 1.4788
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.333e+00 5.487e-01 9.720 1.59e-12 ***
## area 4.850e-04 8.657e-05 5.602 1.29e-06 ***
## peri -1.527e-03 1.770e-04 -8.623 5.24e-11 ***
## shape 1.757e+00 1.756e+00 1.000 0.323
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8521 on 44 degrees of freedom
## Multiple R-squared: 0.7483, Adjusted R-squared: 0.7311
## F-statistic: 43.6 on 3 and 44 DF, p-value: 3.094e-13其中shape变量不显著。 可能的原因有:
- shape与因变量没有关系;
- 样本量不足;
- shape与因变量之间有非线性关系,该非线性无法用线性近似。
用样条平滑的gam()建模:
## 载入需要的程辑包:nlme## Warning: 程辑包'nlme'是用R版本3.6.3 来建造的##
## 载入程辑包:'nlme'## The following object is masked from 'package:dplyr':
##
## collapse## This is mgcv 1.8-31. For overview type 'help("mgcv-package")'.##
## Family: gaussian
## Link function: identity
##
## Formula:
## log(perm) ~ s(area) + s(peri) + s(shape)
##
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.1075 0.1222 41.81 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(area) 1.000 1.000 29.13 1.96e-06 ***
## s(peri) 1.000 1.000 71.30 4.12e-12 ***
## s(shape) 1.402 1.705 0.58 0.425
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.735 Deviance explained = 75.4%
## GCV = 0.78865 Scale est. = 0.71631 n = 48对gam()回归结果做单个变量的曲线拟合图:
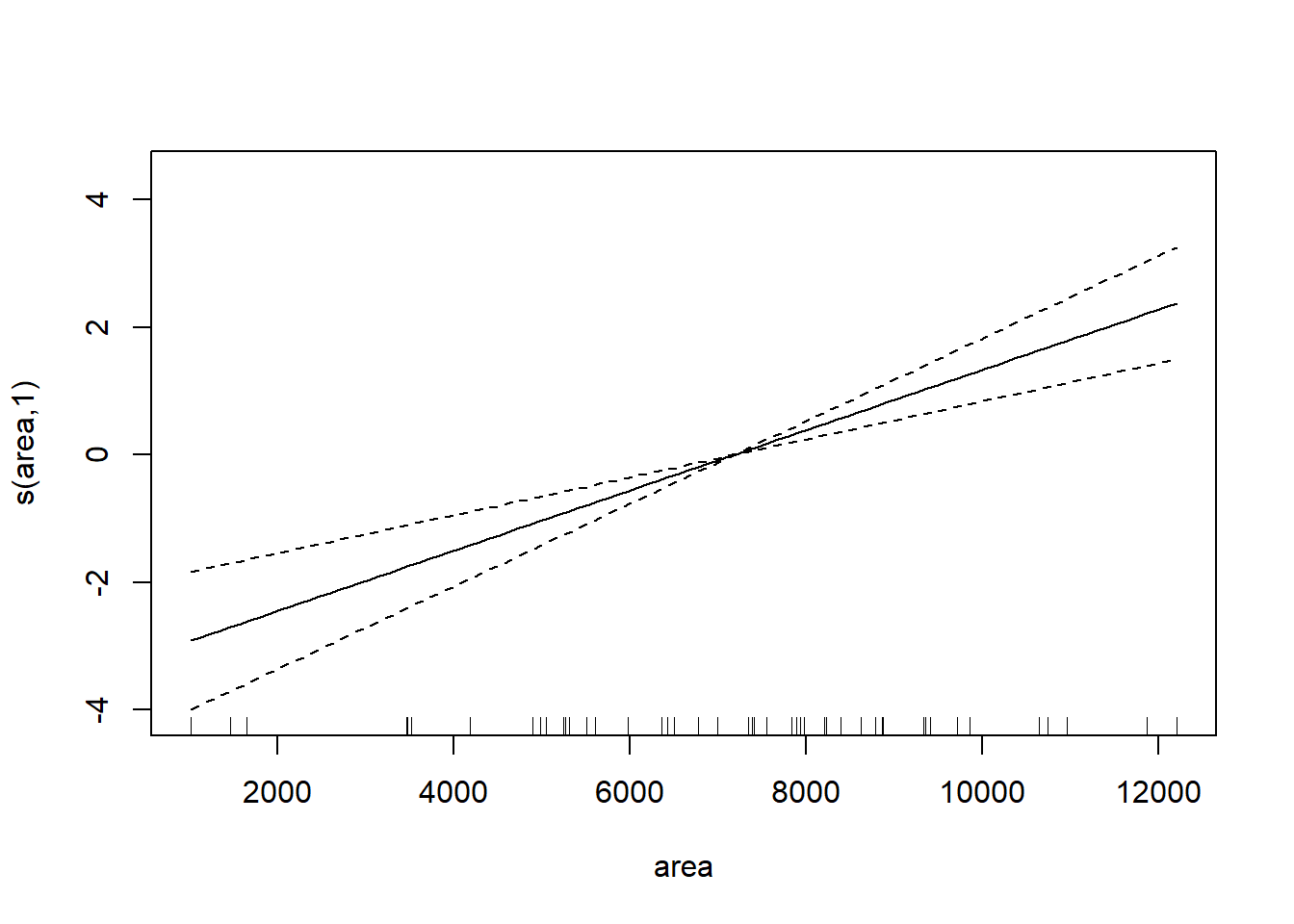
图32.14: 渗透率gam建模
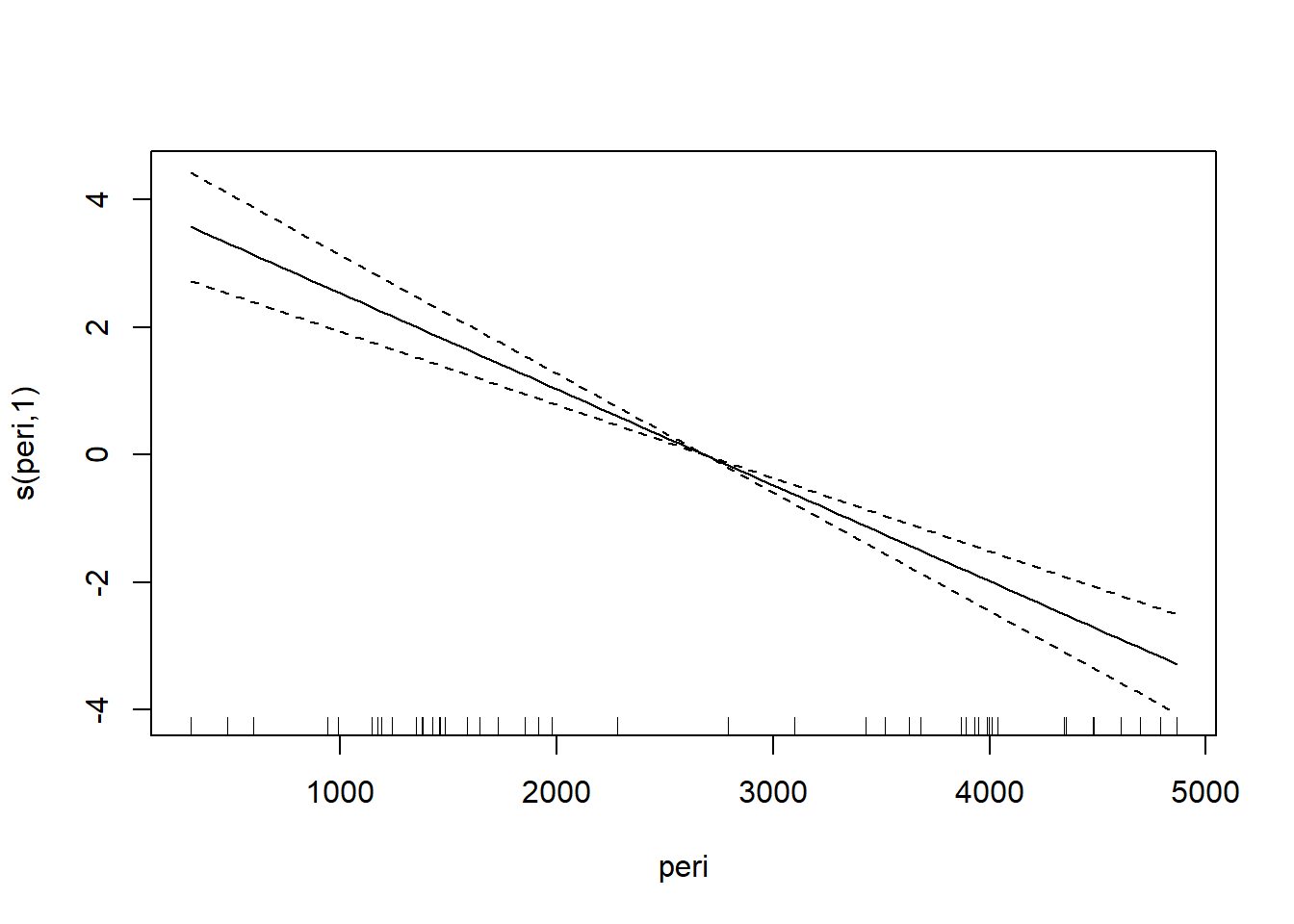
图32.15: 渗透率gam建模
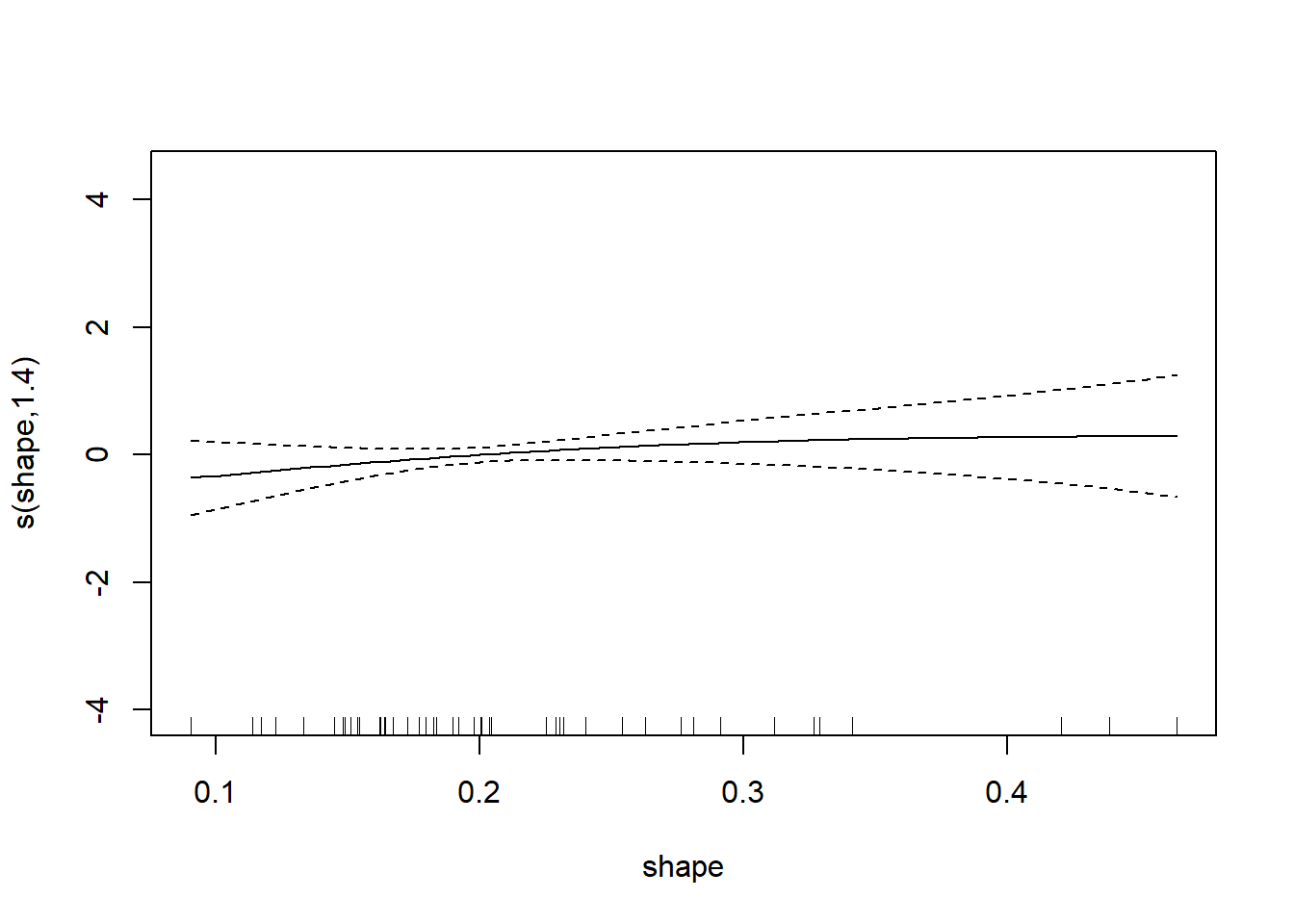
图32.16: 渗透率gam建模
可以看出三条曲线都基本不需要非线性。 比较两个模型:
## Analysis of Variance Table
##
## Model 1: log(perm) ~ area + peri + shape
## Model 2: log(perm) ~ s(area) + s(peri) + s(shape)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 44.000 31.949
## 2 43.598 31.230 0.40237 0.71914 2.4951 0.125结果也不显著, 说明线性模型是可取的。
32.5 Logistic回归
32.5.1 模型
当因变量\(Y\)是零壹变量时,即\(Y\)表示分两类的类别,取值1和0, 我们关心的是\(P(Y=1)\)。这是一个\([0,1]\)区间内的值。 如果把\(Y\)当作一般因变量做线性回归, 会给出不合理的结果,比如负值, 另外线性回归假定误差项为正态分布在这里也不适用。
为此考虑广义的回归模型(广义线性模型): \[\begin{aligned} Y \sim & F(y;\theta) \\ g(\theta) =& \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \end{aligned}\]
特别地,定义logit函数 \[ \text{logit}(p) = \ln \left( \frac{p}{1-p} \right) \]
Logit模型: \[\begin{aligned} Y \sim& b(1, p) \\ \text{logit}(p) =& \beta_0 + \beta_1 X_1 + \dots + \beta_p X_p \end{aligned}\]
32.5.2 R程序
进行logistic回归的R程序如glm(y ~ x1 + x2, family=binomial, data=d),
其中y为取0或1的向量,输入数据集为d。
y也可以是一个两列的矩阵,第一列为成功数,第二列为失败数。
例如,“remiss.csv”中保存了癌症病人康复的数据, 变量remiss为康复与否(1为康复,0为未康复), 另外的6个变量为可能影响康复概率的自变量。
程序:
d.remiss <- read.csv("remiss.csv", header=TRUE)
glm1 <- glm(
remiss ~ cell+smear+infil+li+blast+temp,
family=binomial, data=d.remiss)
summary(glm1)##
## Call:
## glm(formula = remiss ~ cell + smear + infil + li + blast + temp,
## family = binomial, data = d.remiss)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.95165 -0.66491 -0.04372 0.74304 1.67069
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 58.0385 71.2364 0.815 0.4152
## cell 24.6615 47.8377 0.516 0.6062
## smear 19.2936 57.9500 0.333 0.7392
## infil -19.6013 61.6815 -0.318 0.7507
## li 3.8960 2.3371 1.667 0.0955 .
## blast 0.1511 2.2786 0.066 0.9471
## temp -87.4339 67.5735 -1.294 0.1957
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 34.372 on 26 degrees of freedom
## Residual deviance: 21.751 on 20 degrees of freedom
## AIC: 35.751
##
## Number of Fisher Scoring iterations: 8以p值0.30为界限,逐步删去不显著的自变量:
glm1b <- glm(
remiss ~ cell + smear + infil + li + temp,
family=binomial, data=d.remiss)
summary(glm1b)##
## Call:
## glm(formula = remiss ~ cell + smear + infil + li + temp, family = binomial,
## data = d.remiss)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.93753 -0.65855 -0.04328 0.75287 1.65475
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 57.128 69.977 0.816 0.414
## cell 24.180 47.257 0.512 0.609
## smear 18.370 56.218 0.327 0.744
## infil -18.477 59.260 -0.312 0.755
## li 3.987 1.902 2.097 0.036 *
## temp -86.137 64.785 -1.330 0.184
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 34.372 on 26 degrees of freedom
## Residual deviance: 21.755 on 21 degrees of freedom
## AIC: 33.755
##
## Number of Fisher Scoring iterations: 8##
## Call:
## glm(formula = remiss ~ cell + infil + li + temp, family = binomial,
## data = d.remiss)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.88516 -0.66796 -0.07282 0.78697 1.72442
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 70.6171 59.1148 1.195 0.2323
## cell 9.1434 7.9124 1.156 0.2479
## infil 0.9088 3.1356 0.290 0.7719
## li 3.9005 1.8108 2.154 0.0312 *
## temp -85.2481 64.0897 -1.330 0.1835
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 34.372 on 26 degrees of freedom
## Residual deviance: 21.869 on 22 degrees of freedom
## AIC: 31.869
##
## Number of Fisher Scoring iterations: 7##
## Call:
## glm(formula = remiss ~ cell + li + temp, family = binomial, data = d.remiss)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.02043 -0.66313 -0.08323 0.81282 1.65887
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 67.634 56.888 1.189 0.2345
## cell 9.652 7.751 1.245 0.2130
## li 3.867 1.778 2.175 0.0297 *
## temp -82.074 61.712 -1.330 0.1835
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 34.372 on 26 degrees of freedom
## Residual deviance: 21.953 on 23 degrees of freedom
## AIC: 29.953
##
## Number of Fisher Scoring iterations: 7或可用逐步回归:
glm2 <- step(glm(
remiss ~ cell + smear + infil + li + blast + temp,
family=binomial, data=d.remiss))## Start: AIC=35.75
## remiss ~ cell + smear + infil + li + blast + temp
##
## Df Deviance AIC
## - blast 1 21.755 33.755
## - infil 1 21.857 33.857
## - smear 1 21.869 33.869
## - cell 1 22.071 34.071
## <none> 21.751 35.751
## - temp 1 23.877 35.877
## - li 1 26.095 38.095
##
## Step: AIC=33.76
## remiss ~ cell + smear + infil + li + temp
##
## Df Deviance AIC
## - infil 1 21.858 31.858
## - smear 1 21.869 31.869
## - cell 1 22.073 32.073
## <none> 21.755 33.755
## - temp 1 24.198 34.199
## - li 1 30.216 40.216
##
## Step: AIC=31.86
## remiss ~ cell + smear + li + temp
##
## Df Deviance AIC
## - smear 1 21.953 29.953
## <none> 21.858 31.858
## - temp 1 24.292 32.292
## - cell 1 24.477 32.477
## - li 1 30.434 38.434
##
## Step: AIC=29.95
## remiss ~ cell + li + temp
##
## Df Deviance AIC
## <none> 21.953 29.953
## - temp 1 24.341 30.341
## - cell 1 24.648 30.648
## - li 1 30.829 36.829##
## Call:
## glm(formula = remiss ~ cell + li + temp, family = binomial, data = d.remiss)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.02043 -0.66313 -0.08323 0.81282 1.65887
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 67.634 56.888 1.189 0.2345
## cell 9.652 7.751 1.245 0.2130
## li 3.867 1.778 2.175 0.0297 *
## temp -82.074 61.712 -1.330 0.1835
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 34.372 on 26 degrees of freedom
## Residual deviance: 21.953 on 23 degrees of freedom
## AIC: 29.953
##
## Number of Fisher Scoring iterations: 7